Why compiling a mathematical expression?

Back in the "old" days it was common to use assembly language for opimizing the source code of an application. One would take a time critical function and turn it into optimized assembly code thus gaining somewhat around 30% - 200% in speed. If you buy an assembly book it will probably still tell you this is the case nowadays. But the sad fact is that it has become very hard to write assembly code that is more efficient than what a modern compiler can generate when beeing run with all optimizations turned on and if you're not very familiar with the Intel processors optimization guide you will most likely not succeed in outperforming any modern C/C++ compiler with handcrafted assembly code.

Today even the SSE instruction set is readily available from within C++ on any modern platform so why bother learning assembly anyway? One of the possible answers is that if you are writing an interpreter of any kind and if you would like to boost it's performance by using a just in time compiler you will most likely need assembly language. Compiled code is still an order of a magnitude faster than interpreted code even if it is highly optimized code.

A modern CPU's Streaming SIMD Extension (SSE) provides a set of 8 registers useable for fast mathematical operations with floating point numbers. Their main purpose is to allow performing multiple operations at once by packing up to 4 numbers into the registers and operating simultaneously with all 4 values. The SSE instruction set also contains instructions for working with single floating point numbers. These instructions are prefixed with "ss" since they operate with single scalar values. This is the instruction subset predominantly used by muparserSSE (i.e. movss, divss, mulss, addss, subss, ...)

The reverse polish notation

In order to understand how muParserSSE works you first need to understand what a reverse polish notation is. Reverse Polish notation (or just RPN) is a mathematical notation wherein every operator follows all of its operands. Got that? Probably not so lets explain it with a bit more detail. The way a mathematical expression is normaly presented is called the infix notation. You probaly did'nt know that but believe me if you have ever attended a math lesson you have seen an expression in infix notation. Operators are written between the operands and you can use parentheses in order to define an evaluation order.

A simple Expression

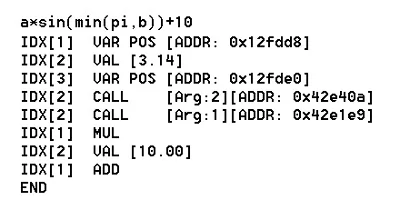
In order to demonstrate how the evaluation works, lets look at sample expressions. Our first sample is a simple expression without functions and with few binary operators:

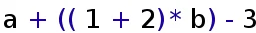Expression 1: A simple mathematical expression. Operator items are colored blue, value items are colored in black.

Nothing special about that. Infix notation is a "human friendly" way to write an expression. Unfortunately to calculate it using a computer one needs a "computer friendly" way to write the expression and the reverse polish notation (or postfix notation) is just that. The RPN of our sample above looks like:

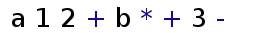Expression 1a: The reverse polish notation of expression 1.

Explaining how tor translate infix notation into postfix notation is beyond the scope of this article but if you are interested have a look at the Shunting-yard algorithm. For now just lets assume you already have the RPN of your expression. The expression is evaluated from left to right. Each value or variable is pushed to a stack. If an operator is found, it is executed taking the two uppermost vaues from the stack as its arguments and pushing the result back to the stack.

Lets assume our calculation stack is represented by an array called s and we parse the RPN from left to right. The following scheme then shows all operations required to compute the final result of expression 1:

a : s[0] = a
1 : s[1] = 1
2 : s[2] = 2
+ : s[1] = s[1] + s[2]
b : s[2] = b
* : s[1] = s[1] * s[2]
+ : s[0] = s[0] + s[1]
3 : s[1] = 3
- : s[0] = s[0] - s[1]

The final result is located at s[0] ready for retrieval. A straightforward implementations would allocate an array for s and compute all the necessary steps pretty much like shown above. This is what muparser ist doing. So how can this be translated into assembly language for usage with asmjit?

It's gotta be fast so I intend to use the SSE instruction set. The SSE extension provides 8 additional registers on 32 bit machines. These are: xmm0, xmm1, .., xmm7. I could create an array much like s above and store the values there. Then I could load the values into the SSE registers from there, apply an operation (i.e. addition) and put the result back to my stack array. It would require only 2 SSE registers and a lot of data movement. All in all not very efficient! A better solution would be to use the SSE registers as much as possible. So why not use the registers directly as the calculation stack? There would be no memory allocations, no data movements. It would be very efficient. Lets look at pseudo assembly code usig SSE instructions for computing our sample expression:

a : movss xmm0, a
1 : movss xmm1, 1
2 : movss xmm2, 2
+ : addss xmm1, xmm2
b : movss xmm2, b
* : mulss xmm1, xmm2
+ : addss xmm0, xmm1
3 : movss xmm1, 3
- : subss xmm0, xmm1

This is pretty much a 1:1 translation of the pseudocode given above just with differing syntax. Keep in mind that this is only pseudo assembly code and some details were omitted in order to make it easier to understand. You can not feed this directly into a compiler (although it's close to what you could write using inline assembly)!

To explain it a bit: movss is an instruction moving a floating point value into an SSE register. The instructions addss, mulss and subss perform addition, multiplication and subtraction using the values in the given registers as their input and storing the result in the register used as the first argument. Once the calculation is done the final result would be located in the register xmm0 ready for retrieval. Lets have a look at how this would look like in memory. For the following illustration we assume a=1 and b=2:

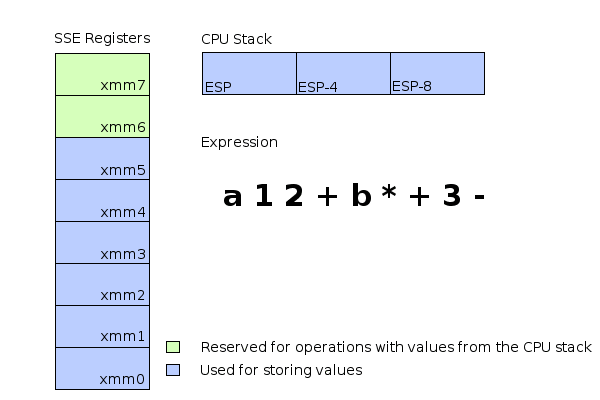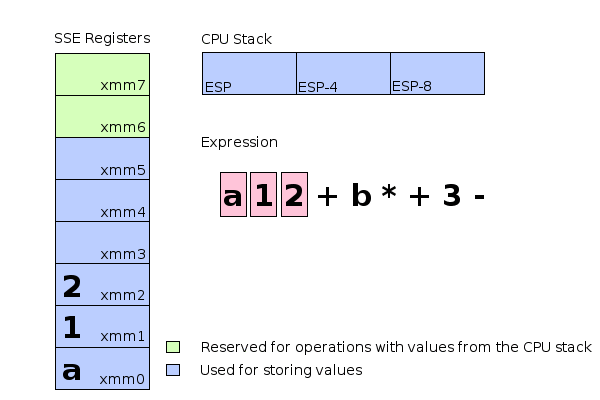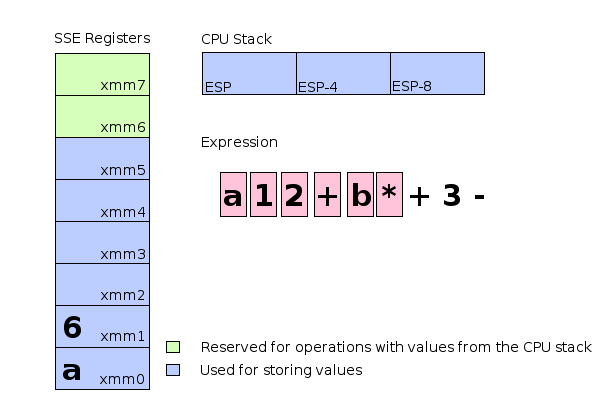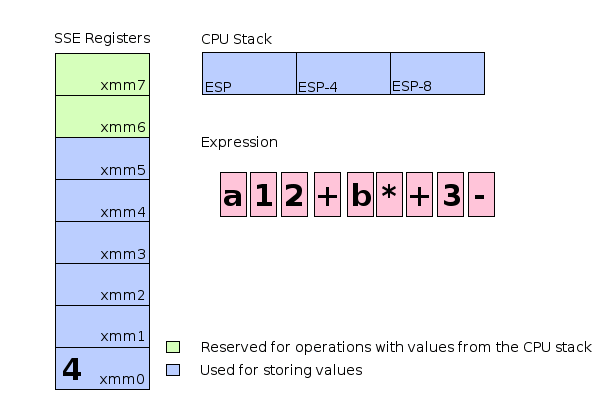Schematic memory and register usage during evaluation of the expression a+((1+2)*b)-3. The entire calculation can be performed exclusively by using SSE registers (xmm0..xmm2).

Creating this set of instructions on the fly from an RPN using asmjit is no big deal. However there are only 8 SSE registers available in total. Will this be enough to deal with any expression? Lets look at another sample.

A slightly more complex Expression

The next expression is slightly more complex. This expression doesn't have functions either and still just uses basic binary operators only. It is using a lot of paranthesis though in order to enforce a certain evaluation order.

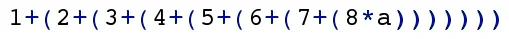Expression 2: A slightly more complex equation using lots of paranthesis.

and its RPN:

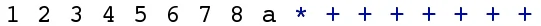Expression 2a: Reverse polish notation of expression 2.

Translating Expression 2a into pseudo assembly using the same approach as for expression 1 would give the following code:

1 : movss xmm0, 1
2 : movss xmm1, 2
3 : movss xmm2, 3
4 : movss xmm3, 4
5 : movss xmm4, 5
6 : movss xmm5, 6
7 : movss xmm6, 7
8 : movss xmm7, 8
a : movss xmm8, a     ; Note: we don't have a register xmm8!
* : mulss xmm7, xmm8  ; Note: we don't have a register xmm8!
+ : addss xmm6, xmm7
+ : addss xmm5, xmm6
+ : addss xmm4, xmm5
+ : addss xmm3, xmm4
+ : addss xmm2, xmm3
+ : addss xmm1, xmm2
+ : addss xmm0, xmm1

Looks great except it does not work that way! There are only 8 SSE registers available but we would need 9 in order to evaluate this expression. So it's obvious that given an arbitrarily complex expression there is no way to store all values in SSE registers. We have to find another solution!

How about this: The lowermost 6 registers (xmm0, xmm1, ..., xmm5) are used for directly storing values. They serve as the calculation stack. If a value needs to be stored at a higher position it's stored directly on the CPU stack. For instance if all 6 registers are occupied and another value needs to be pushed to the calculation stack 4 additional bytes are allocated on the CPU stack by decreasing ESP by 4 bytes and the value is stored at this location instead. The two remaining SSE registers (xmm6 and xmm7) are used for performing operations with values stored on the CPU stack.

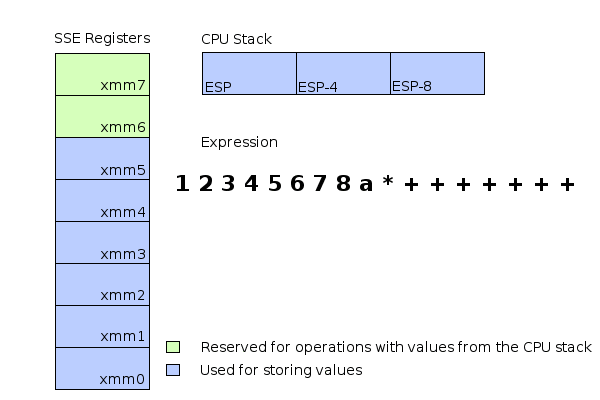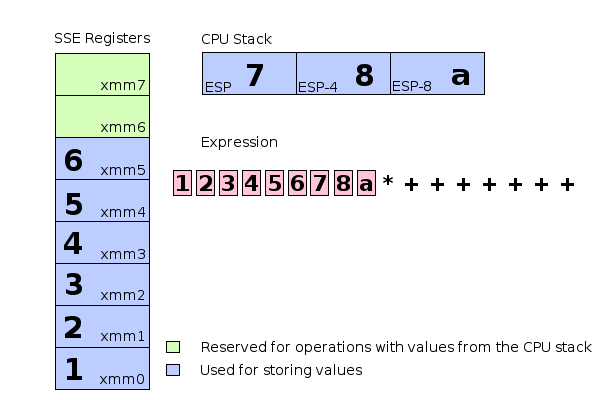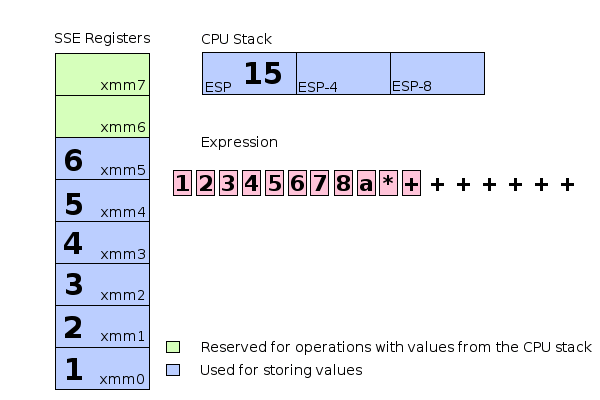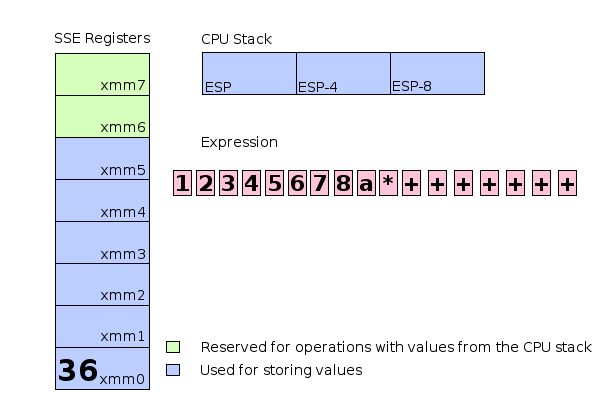Schematic memory and register usage during evaluation of the expression 1+(2+(3+(4+(5+(6+(7+(8*a))))))).

The illustration above shows how complex expressions can be evaluated using a combination of SSE register commands and stack allocations. Extending this mechanism to support function calls is relatively easy. This library supports only callbacks with the cdecl calling convention. Arguments are pushed to the stack from right to left and the calling function has to clean up the stack afterwards.

Benchmarks

The whole point of creating muparserSSE was to improve evaluation performance. But making precise estimates over the gain in performance from muparserSSE is not easy. The performance can be an order of a magnitude better when the expression doesn't contain functions. It can be faster by factor 2 to 5 when functions are used and in some cases there is no benefit at all. There is still room for improvement in muparserSSE so i won't claim it's generating the fastest possible machine code. However its significantly faster than math parsers based on interpretation rather than compilation and it's not slower than MathPresso the only other free math parser using a just in time compiler. The following parsers were used in the benchmark:

• fparser - Function Parser for C++ v4.2
• MTParser - An extensible math expression parser with plug-ins
• muParser - a fast math parser library

• MathPresso - A Math expression parser from the author of asmjit
• muparserSSE - A math expression compiler

In order to conduct the benchmarks I set up a small application containing all of the math parsers with their source code. This was done in order to guarantee all use the same optimized compiler settings such as:

• use of intrinsic functions
• creation of SSE instructions
• fast floating point modell
• omit frame pointer
• inlining of all suitable functions
• highest optimization level
• no buffer safety checks

The results are shown in the following two diagrams:

Performance of different open source math parser for a set of random expressions without functions.

Performance for a set of random expressions with functions.