A fast math expression parser capable of parallel expression evaluation.

This library depends on the Standard template library (STL). The problem with the STL is that every C++ compiler has its own implementation of the STL and different STL implementations are not compatible in terms of their memory layout. Since STL template classes are used in the API of muParserX I do not see a maintainable way to provide a prebuild library. Your only choice of using the library is adding its source code directly to your project.
In order to use the library you should add all files located in the "muparserx/parser" subdiretory into your own project. The library currently comes with CMake based build system but It should compile on every standard compliant C++ (C++11 and above) compiler.
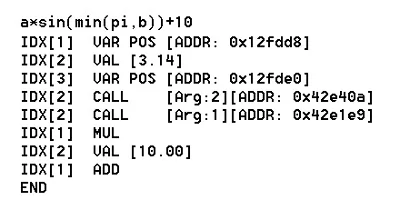
Before starting I should give you an overview over the classes related to muParserX. Parsing works by splitting the mathematical expression into so called tokens. A token can be either a value, a variable, a function call, an operator or a special character such as brackets or commas. The tokens will be stored internally for processing during the evaluation process. When using the parser you will deal with tokens directly only when setting variables, constants functions or operators.
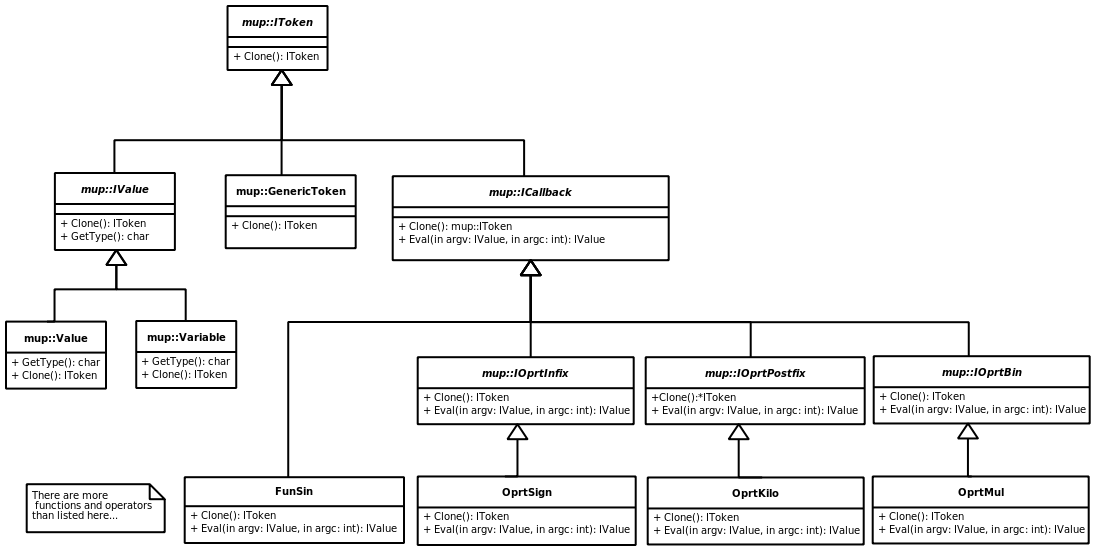 Image 1: Token hierarchy of the parser.
Image 1: Token hierarchy of the parser.
The parser defines an abstract base class named mup::IToken from which all of its tokens are derived. There are three major kinds of token: Value tokens, Callback tokens and generic tokens. Values represent either constants or variables, callbacks represent functions and operators, generic tokens are used for brackets, commas and special characters.
It's important to know that muParserX handles its tokens via reference counted smart pointers using the mup::TokenPtr<...> template class. There is no need to release their pointers explicitely with the delete operator. The following typedefs represent smart pointer names:
namespace mup
{
// Type of a managed pointer storing parser tokens via their base type.
typedef TokenPtr<IToken> ptr_tok_type;
// Type of a managed pointer storing value tokens via their base type.
typedef TokenPtr<IValue> ptr_val_type;
// Type of a managed pointer storing binary operator tokens.
typedef TokenPtr<IOprtBin> ptr_binop_type;
}
In order to use muParserX you have to include the file mpParser.h into your projects. The parser resides in the namespace mup.
#include "mpParser.h"
using namespace mup;
The parser functionality is organized in so called packages. A package consist of a set of predefined mathematical functions, operators and constants as well as value detection callbacks. Creating a parser instance is simple: The constructor takes an optional variable made up of several flags for activating certain parser packages. For convenience the parser already defines the enumeration values pckALL_COMPLEX and pckALL_NON_COMPLEX which can be used to configure the parser for either complex valued calculation or noncomplex calculations. If this parameter is omitted the parser will be run in its default mode which means it is using complex numbers and all available operators and functions will be installed (pckALL_COMPLEX).
ParserX p(pckALL_NON_COMPLEX);Each parser package is encoded with a certain bit. The following values and value combinations can be used for activating or deactivating certain parser packages at construction time:
| Package enumerator | Numeric value | Description |
|---|---|---|
| pckCOMMON | 1 | Installs common functionality such as binary operators and basic functions. |
| pckUNIT | 2 | Installs postfix operators for scaling to mimic basic unit support. |
| pckCOMPLEX | 4 | Installs complex valued functions, operators and the imaginary unit *i* as a parser constant. The packages pckCOMPLEX and pckNON_COMPLEX are mutually exclusive. |
| pckNON_COMPLEX | 8 | Installs noncomplex functions and operators. The packages pckCOMPLEX and pckNON_COMPLEX are mutually exclusive. |
| pckSTRING | 16 | Adds function for string processing as well as the capability to detect string values. |
| pckMATRIX | 32 | Adds functions and operators for matrix support. |
| pckALL_COMPLEX | pckCOMMON | pckCOMPLEX | pckSTRING | pckUNIT | combines the flags of packages useable with complex numbers. |
| pckALL_NON_COMPLEX | pckCOMMON | pckNON_COMPLEX | pckSTRING | pckUNIT | Combines the flags of all packages useable with noncomple numbers. |
muParserX defines a common interface for classes representing Values. This interface is implemented by the classes mup::Value and mup::Variable.
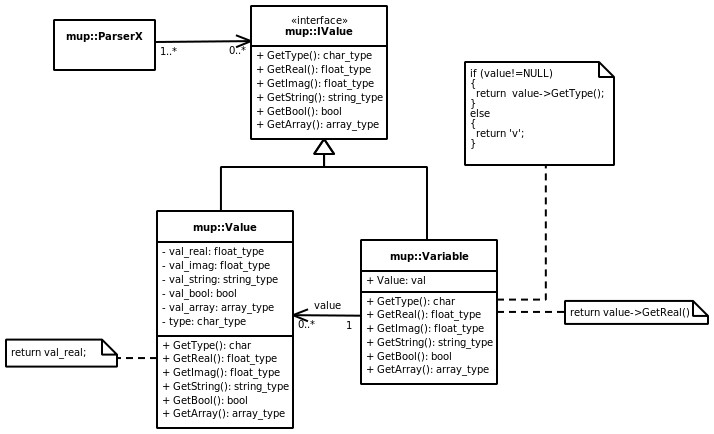 Image 2: Value and Variable classes of the parser.
Image 2: Value and Variable classes of the parser.
mup::Value is a variant type class able to store different data types in a single object. If you want to set up a value for use with muParserX you first have to wrap it into an object of this type. Then you need to bind the value to a mup::Variable object which essentially serves as a proxy for value objects.
Variables can be defined either explicitely in your C++ code or implicitely at parser runtime. Implicit creation of variables is usefull when writing console applications that require dynamic creation of variables (i.e. by using the assignment operator).
In order to create a value for use with muParserX you have to create a value object first. The value class provides overloaded constructors for all relevant types:
using namespace mup;
// ...
// Create a complex variable
Value cVal(cmplx_type(1, 1));
// Create a string variable
Value sVal(_T("Hello World"));
// Creating a floating point variable
Value fVal(1.1);
// Creating an integer variable
Value fVal(1);
// Creating an boolean variable
Value bVal(true);
// Create a 3x3 identity matrix
Value m1(3, 3, 0);
m1.At(0, 0) = 1;
m1.At(1, 1) = 1;
m1.At(2, 2) = 1;
// Create an array
Value arr(2, 0); // Arguments: number of elements, default value
arr.At(0) = 2.0;
arr.At(1) = _T("hallo"); // note that arrays can consits of mixed type elementsOnce you have a parser value you can bind it to a variable object. A variable serves as a proxy class for value objects. It merely holds a pointer to the original value and refers all queries to it thus allowing the parser to change it. After creating the variable object use the DefineVar function in order to add it to the parser. In a similar procedure constants can be defined by using the DefineConst member function but they can be submitted directly.
ParserX p;
Value val( 1.1);
Variable var(&val);
p.DefineVar("a", var);
// Now lets define some constants
p.DefineConst("b", val);
// Alternatively you could simply use:
p.DefineConst("b", 1.1);Once a variable is defined there is no need to call DefineVar again just to change it's value! If you want to change the value change the submitted value object directly. Remember: The parser has a pointer to this value object and it gets the value directly from there! Consequently you have to make sure the value object exists throughout the lifetime of the parser instance that is using it!
Implicit creation of variables refers to the creation of parser variables at parser runtime. With this feature you can create variables on the fly without any additional client code. Since this is usefull only for applications requiring direct user interaction it is turned off by default. In order to use it you have to activate it first by calling the EnableAutoCreateVar member function:
ParserX p;
p.EnableAutoCreateVar(true);
// Lets set up an expression for defining a new variable named "a" with the value 123
p.SetExpr("a=123");
// The call to Eval() will create the variable internally
p.Eval();
Once you have activated the automatic creation of variables the parser will add a variable every time it finds unknown input that could represent
a variable name without actually having a definition for such a variable. For instance an expression like a=10 would automatically create a new
variable named a provided the variable isn't defined already.
It's recommended to always use this feature together with the assignment operator
in order to initialize the variable with a proper value. If no assignment operator is found the variable is initialized to zero. The downside is
that a statement like abc would also create a variable if there is not already one with that name defined.
After setting up the variables properly, you can use the SetExpr member function of muParser to define the expression. The next thing
you have to do is call Eval to evaluate the expression. The return value is stored in an object of type mup::Value. The complete code for
creating variables, setting up the expression and evaluating the result is shown here:
// Create the parser instance
ParserX p;
// Create an array of mixed type
Value arr(3, 0);
arr.At(0) = 2.0;
arr.At(1) = "this is a string";
// Create some basic values
Value cVal(cmplx_type(1, 1));
Value sVal("Hello World");
Value fVal(1.1);
// Now add the variable to muParser
p.DefineVar("va", Variable(&arr));
p.DefineVar("a", Variable(&cVal));
p.DefineVar("b", Variable(&sVal));
p.DefineVar("c", Variable(&fVal));
p.SetExpr("va[0]+a*strlen(b)-c");
for (int i=0; i<<10; ++i)
{
// evaluate the expression and change the value of
// the variable c in each turn
cVal = 1.1 * i;
Value result = p.Eval();
// print the result
console() << result << "\n";
}Sometimes it is necessary to get a list of all variables or constants currently defined by muParserX. You may either want to query all variables or just the variables used in an expression. The latter may be usefull when you are dealing with a large number of variables and it's not possible to define all of them before evaluating an expression.
To get the list of all variables currently defined by an instance of muParserX use the ParserX::GetVar() member function. It returns a
map containing the variable names as the keys and pointers to the variable tokens as the values. In order to further process the variable you should
cast the token into its proper type (mup::Variable) as shown in the following sample:
// Get a map of all variables used by muParserX
var_maptype vmap = parser.GetVar();
for (var_maptype::iterator item = vmap.begin(); item!=vmap.end(); ++item)
cout << item->first << "=" << (Variable&)(*(item->second)) << "\n";
Getting the expressions used in an expression does work the same way except that you have to use the ParserX::GetExprVar() member function
instead of ParserX::GeVar(). Querying the expression variables does only make sense after having set up an expression using ParserX::SetExpr(...).
// Set the expression
parser.SetExpr("a*sin(b)");
// Query the expression variables
var_maptype vmap = parser.GetExprVar();
for (var_maptype::iterator item = vmap.begin(); item!=vmap.end(); ++item)
cout << " " << item->first << " = " << (Variable&)(*(item->second)) << "\n";
Querying all parser constants works the same way by using ParserX::GetConst() member function:
// Get a map containing all constants
val_maptype cmap = parser.GetConst();
for (val_maptype::iterator item = cmap.begin(); item!=cmap.end(); ++item)
cout << " " << item->first << " = " << (Value&)(*(item->second)) << "\n";
All custom functions must implement the ICallback interface. This interface provides the ICallback::Clone(), ICallback::Eval(...) and ICallback::GetDesc() member functions. An implementation of a user defined class may look like this:
class MySine : public mup::ICallback<
{
MySine()
:ICallback(cmFUNC, "mysin", 1)
{}
virtual void Eval(ptr_val_type &ret, const ptr_val_type *a_pArg, int a_iArgc)
{
// Get the argument from the argument input vector
float_type a = a_pArg[0]->GetFloat();
// The return value is passed by writing it to the reference ret
*ret = sin(a);
}
const char_type* GetDesc() const
{
return "mysin(x) - A custom sine function";
}
IToken* Clone() const
{
return new MySine(*this);
}
};The mup::ICallback constructor takes three argument. The first determines the type of the callback. If you want to add a parser function use cmFUNC. The second is the function name and the last parameter is the number of arguments.
The implementation of your callback has to be done in the Eval function. Eval takes three parameters. The first one is a reference to a smart pointer of type IValue holding the return value. The second one is a pointer to an array containing the function arguments. These arguments are also passed via a smart pointer. The last argument is the number of arguments.
By using the member functions implemented by the IValue interface you can easily access the values and perform the actual work. In this sample the first (and only) argument is interpreted as a double value, its sine is calculated and it is then written to the return value.
float_type a = a_pArg[0]->GetFloat();
*ret = sin(a);Please note that the parser leaves the type checking of the function arguments entirely to your implementation of ICallback::Eval. The mechanism for implementing callback functions is always the same. Binary operators are treated like functions taking two arguments, unary operators like functions with a single argument.
After implementing the logic you have to register it with muParserX by using the DefineFun member function:
ParserX p;
p.DefineFun(new MySine);One important thing to note is that once submitted to DefineFun the parser takes ownership of the newly created pointer. You may not release it on your own! The parser will release it!
Defining your own operators is very similar to defining new functions. You have to create a callback object and register it at the parser instance. The parser lets you add unary operators (both infix and prefix) as well as binary operators using the following member functions:
void DefineOprt(IOprtBin *a_pCallback)
void DefinePostfixOprt(IOprtPostfix *a_pCallback)
void DefineInfixOprt(IOprtInfix *a_pCallback)As already mentioned binary operators are defined in a very similar manner as function definitions. The main difference is that you don't have to implement the ICallback interface directly but use it indirectly by implementing the IOprtBin interface which itself is derived from ICallback. IOprtBin is an Extension to ICallback able to handle precedence and associativity parameters needed by binary operators. Consequently you need additional parameters for the construction of binary operators: operator precedence and operator associativity.
Operator precedence is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression. The precedence value for in muParserX is a simple integer value. The higher the value, the higher the priority of the operation. For instance if you want to compute the following expression properly:
2 + 3 * 4Then you need to make sure that the addition has a lower precedence than the multiplication. So basically what you are calculating is
(3 * 4) + 2 = 14In order to do this you can use the predefined precedence values as defined by muParserX in the enumerator EOprtPrecedence. This enumerator does not only contain precedence values for binary operators but also for unary operatory and the ternary if-then-else operator:
enum EOprtPrecedence
{
prASSIGN = -1,
prIF_THEN_ELSE = 0,
prLOGIC_OR = 1,
prLOGIC_AND = 2,
prBIT_OR = 3,
prBIT_AND = 4,
prRELATIONAL1 = 5, // For "==", "!="
prRELATIONAL2 = 6, // Relational operators "<", "<=", ">", ">="
prSHIFT = 7, // Shift operators "<<", ">>"
prADD_SUB = 8, // addition
prMUL_DIV = 9, // multiplication/division
prPOW = 10, // power operator priority (highest)
prINFIX = 9, // Signs have a higher priority than ADD_SUB, but lower than power operator
prPOSTFIX = 9 // Postfix operator priority (currently unused)
};The operator associativity is a parameter that determines how operators of the same precedence are grouped in the absence of parentheses. It can either be right associative or left associative. For instance lets have a look at the following expression:
5^4^3^2Depending on the operator associativity this expression could either be interpreted as
5^(4^(3^2))which correctly implements the power operator as a right associative operator or alternatively one could also evaluate:
((5^4)^3)^2Which would (incorrectly) ignore the right associativity of the power operator and compute a different result.
By putting this information together we can now implement a simple binary operator for the addition of noncomplex scalar values:
class OprtAdd : public IOprtBin
{
public:
OprtAdd::OprtAdd()
:IOprtBin(_T("+"), (int)prADD_SUB, oaLEFT)
{}
virtual void Eval(ptr_val_type &ret, const ptr_val_type *a_pArg, int)
{
const IValue *arg1 = a_pArg[0].Get();
const IValue *arg2 = a_pArg[1].Get();
if (!arg1->IsNonComplexScalar())
throw ParserError( ErrorContext(ecTYPE_CONFLICT_FUN, -1, GetIdent(), arg1->GetType(), 'f', 1));
if (!arg2->IsNonComplexScalar())
throw ParserError( ErrorContext(ecTYPE_CONFLICT_FUN, -1, GetIdent(), arg2->GetType(), 'f', 2));
*ret = arg1->GetFloat() + arg2->GetFloat();
}
virtual const char_type* OprtAdd::GetDesc() const
{
return _T("x+y - Addition for noncomplex values");
}
virtual IToken* OprtAdd::Clone() const
{
return new OprtAdd(*this);
}
};