Genauigkeit numerischer Integrationsverfahren

Einführung

In diesem Artikel werden anhand von zwei Simulationsbeispielen verschiedene numerische Verfahren verglichen. Im ersten Teil wird am Beispiel des gedämpften harmonischen Oszillators genauer auf den Einfluss der Schrittweite auf den Gesamtrechenfehler eingegangen. Dieses Problem ist analytisch lösbar und eignet sich daher für eine genaue Quantifizierung des Gesamtfehlers.

Der zweite Teil beschäftigt sich erneut mit dem Magnetpendel. Das dort beschriebene Problem ist chaotischer Natur. Daher erfolgt hier der Vergleich nicht mit einer analytischen Lösung, sondern zwischen den Lösungen der verschiedenen Integrationsverfahren. Dieser Artikel soll den Leser für die Problematik der Zeitschrittwahl sensibilisieren und vor allem mit dem häufig anzutreffenden Irrtum aufräumen man müsste die Zeitschritte nur klein genug wählen um letztendlich ein genaues Ergebnis zu bekommen.

Um diesen Artikel zu verstehen sind Grundkenntnisse der in numerischer Integration von Vorteil. Es wäre hilfreich, wenn Leser bereits mit Euler, Runge-Kutta und Adams-Bashforth Verfahren vertraut sind, da ich diese Verfahren hier nicht näher erläutern werde. Wer mehr über Runge-Kutte Verfahren lernen möchte, dem empfehle ich folgenden Artikel:

Das Runge Kutta Verfahren
Detailierte Einführung in das Runge-Kutta Verfahren 4. Ordnung

Genauigkeit von Integrationsverfahren

Die Genauigkeit eines Integrationsverfahrens wird durch den lokalen Fehler und den globalen Fehler bestimmt. Der lokale Fehler ist der Fehler, der bei einem einzelnen Integrationsschritt auftritt. Der globale Fehler ergibt sich aus der Summe der lokalen Fehler von vielen Integrationsschritten. Normalerweise werden Landau-Symbole verwendet um den lokalen und globalen Fehler anzugeben. Man spricht auch von der Ordnung eines Verfahrens (engl.: big O notation). Der maximale Fehler eines Verfahrens der Ordnung p (für kleine Schrittweiten h) ist eine Funktion proportional zu h^p oder mit Landau-Symbolen: O(h^p). Prinzipiell gilt: Je größer die Ordnung p, desto besser ist das Integrationsschema.

Verfahrensübersicht

Bei der numerischen Lösung von Anfangswertproblemen unterscheidet man Einschrittverfahren und Mehrschrittverfahren. Einschrittverfahren berechnen ausgehend von einem Ausgangspunkt Lösungen Schritt für Schritt. Sie verwenden dafür lediglich die zuletzt bestimmte Näherung. Mehrschrittverfahren greifen für die Bestimmung der Lösung weiter als einen Zeitschritt zurück. Für diesen Artikel wurden folgende Einschrittverfahren untersucht:

Methodenname	Abkürzung	Lokaler Fehler	Globaler Fehler
Euler	Euler	O(h^2)	O(h)
Modified Euler	Euler mod.	O(h^3)	O(h^2)
Heun Method	Heun	O(h^3)	O(h^2)
Runge-Kutta (3. Ordnung)	RK3	O(h^4)	O(h^3)
Runge-Kutta (4. Ordnung)	RK4	O(h^5)	O(h^4)
Runge-Kutta (5. Ordnung)	RK5	O(h^6)	O(h^5)

Die Gruppe der Mehrschrittverfahren werden hier von Adams-Bashforth Verfahren verschiedener Ordnungen vertreten. Im einzelnen sind dies:

Methodenname	Abkürzung	Lokaler Fehler	Globaler Fehler
Adams-Bashforth (2 Schritt)	ADB2	O(h^3)	O(h^2)
Adams-Bashforth (3 Schritt)	ADB3	O(h^4)	O(h^3)
Adams-Bashforth (4 Schritt)	ADB4	O(h^5)	O(h^4)
Adams-Bashforth (5 Schritt)	ADB5	O(h^6)	O(h^5)
Adams-Bashforth (6 Schritt)	ADB6	O(h^7)	O(h^6)

Das ultimative Ziel einer jeden Simulation ist es, genaue Ergebnisse in einer akzeptablen Zeit zu erlangen. Zunächst steht man also vor der Wahl des Integrationsschemas. Danach muss man die Simulation nur noch mit einer akzeptablen Zeitschrittweite durchführen. Das prinzipielle Problem dabei ist allerdings, dass genauere Integrationsschemen mehr Funktionsauswertungen benötigen als einfachere. Dadurch erhöht sich deren Rechenaufwand. Auf der anderen Seite sind aber Verfahren hoher Ordnung selbst bei größeren Zeitschrittweiten genauer als vergleichbare Verfahren niederer Ordnung. Man hat also die Wahl zwischen einem einfacheren Verfahren mit kleiner Zeitschrittweite und einem aufwendigeren Verfahren mit größerer Zeitschrittweite.

Aber Vorsicht: Die Annahme man kann selbst mit Verfahren niederer Ordnung ein "richtiges" Ergebnis errechnen, wenn man nur die Zeitschrittweite klein genug wählt ist falsch. Um das zu Untermauern sehen wir uns den sogenannten globalen Fehler der Integrationsverfahren einmal genauer an. Die folgenden Eigenschaften eines Integrationsschemas sind direkt von der Zeitschrittweite abhängig:

Genauigkeit der Lösung mit Rundungsfehler (~ 1/h) und Globalem Fehler (~ h^p)
Rechenzeit (~1/h)
Numerische Stabilität

Bild 1 zeigt den absoluten Fehler als Summe von Rundungsfehler und globalem Fehler des Verfahrens. Die Darstellung verwendet eine logarithmische Skala. Globaler Fehler und Rundungsfehler Verhalten sich gegenläufig. Während der globale Fehler für kleine Schrittweiten abnimmt, steigt der Rundungsfehler an. Addiert man die beiden Fehler, so wird deutlich, dass es eine optimale Schrittweite gibt, für die der absolute Fehler minimal wird. Daraus folgt, dass eine zu kleine Schrittweite das Ergebnis infolge der verstärkt auftretenden Rundungsfehler verschlechtert und nicht verbessert.

Bild 1: Absoluter Fehler als Summe von Rundungsfehler und Verfahrensfehler (Globaler Fehler).

Beispielrechnungen

Der gedämpfte harmonische Oszillator

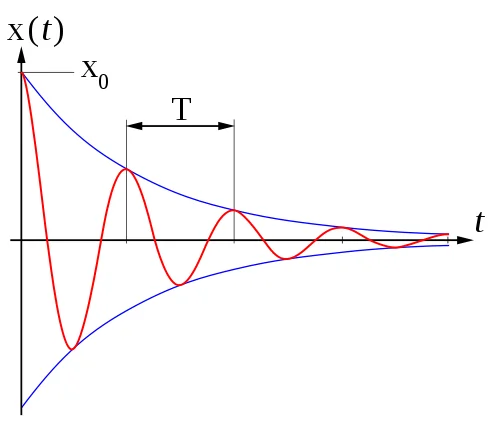
Wenn man eine Integrationsengine implementiert, sollte sie zunächst gegen ein Modell, dessen analytische Lösung bekannt ist getestet werden. In diesem Fall dient das Modell des gedämpften harmonischen Oszillators als Referenz. Dieses Modell wird durch eine homogene Differentialgleichung 2. Ordnung beschrieben:

Schematische Darstellung einer gedämpften Schwingung. (Urheber: Jahobr bzw. Oleg Alexandrov; [1] und [2]) \begin{equation} \nonumber\ddot {x} + {\mu \over m} \dot{x} + {k \over m} x = 0 \label{eq:eqn_of_motion2} \end{equation}

mit:

m - Pendelmasse
\(\mu\) - Reibungskoeffizient
k - Federkonstante

Es sollen folgende Anfangsbedingungen gelten:

\begin{equation} \nonumber x(0)=x_0 \quad \dot{x}(0)=0 \end{equation}

Das Ergebnis dieses Differentialgleichung ist eine Funktion, welche die Position des Oszillators als Funktion der Zeit angibt:

\begin{equation} \nonumber x(t) = x_0 e^{-\delta t} (cos(\omega t) + \frac{\delta}{\omega} sin (\omega t)) \end{equation}

wobei:

\begin{equation} \nonumber \delta = {\mu \over {2m} } \quad,\quad \omega_0 = \sqrt {k \over m} \quad,\quad \omega = \sqrt{\omega_0^2 - \delta^2} \label{eq:omega} \end{equation}

Die Differenz zwischen analytischer Lösung (siehe Bild 3) und simulierter Lösung ist der absolute Fehler. Bild 4 zeigt den Zusammenhang zwischen absolutem Fehler und Zeitschrittweite für verschiedene Integrationsverfahren.

Bild 3: Vergleich zwischen analytischer und simulierter Lösung für eine Zeitschrittweite von h=0.005. Alle Verfahren, außer dem von Euler zeigen gute Übereinstimmung mit der exakten Lösung.

Bild 4: Absoluter Fehler in Abhängigkeit der Integrationsschrittweite für verschiedene Integrationsverfahren.

Es wird deutlich, dass der theoretische Zusammenhang zwischen absolutem Fehler und Zeitschrittweite bestätigt wird. Man kann klar sehen, dass es eine optimale Zeitschrittweite für jedes der Verfahren gibt, bei der der absolute Fehler minimal ist. Man sieht auch, dass die Verfahren höherer Ordnung, wie z.B. RK5 eindeutig am genauesten rechnen. Um so höher die Ordnung der Verfahren, um so geringer werden die absoluten Fehler. Es wird auch deutlich, dass die Verfahren höherer Ordnung das Minimum des absoluten Fehlers erst bei größeren Schrittweiten erreichen.

Wenn man sich auf der anderen Seite nun das Eulerschema ansieht, sieht man, dass das Minimum seines absoluten Fehlers bei sehr kleinen Schrittweiten anzutreffen ist. Obwohl diese Schrittweiten um Größenordnungen kleiner sind, als die der anderen Verfahren ist sein Fehler dennoch am größten. Wenn man dazu noch kurz auf Bild 3 schaut, sieht man auch das das Eulerverfahren selbst bei moderaten Schrittweiten versagt. Was lernen wir daraus?

Eulers Methode war zwar ziemlich Visionär für seine Zeit (1768) aber sie ist einfach nicht mehr das, was man heute noch verwenden sollte. Darüber hinaus zeigt das Beispiel, dass zu kleine Schrittweiten nicht nur eine ziemliche Verschwendung von Computerressourcen sind, sondern das Ergebnis auch noch schlechter machen!

Die Betrachtung der Genauigkeiten ist schön und gut, aber das Verfahren höherer Ordnung genauer sein sollten, ist offensichtlich. Was uns wirklich interessiert ist, ob sie bei vergleichbarer (oder besserer) Genauigkeit auch schneller sind. Sehen wir uns dafür die Rechengeschwindigkeit genauer an. Um die zu analysieren, ist in Bild 5 die Abhängigkeit zwischen Zeitschrittweite und Rechenzeit aufgetragen. Wir sehen einen einfachen Zusammenhang, der aussagt, daß die Rechenzeit mit zunehmende Integrationsschrittweite sinkt. Das ganze dargestellt in einem Satz fast perfekter Geraden, die allerdings keinen linearen Zusammenhang beschreiben, da das Diagramm eine doppelt logarithmische Skalierung verwendet.

Wenn man die Zeitschrittweite halbiert, verdoppelt man gleichzeitig die Anzahl der zu berechnenden Funktionsauswertungen. Man zahlt also einen ziemlich hohen Preis für kleine Zeitschritte, unabhängig davon welche Integrationsmethode man wählt. Da jede Zeitschrittweite auch stellvertretend für eine bestimmte Rechenzeit des Modells steht, kann man ein Diagram erstellen, welches das Quadrat des absoluten Fehler über der Zeitschrittweite darstellt (Bild 6). Hier wird es jetzt interessant, denn man kann jeder Genauigkeit direkt eine Rechenzeit zuordnen.

Bild 5: Abhängigkeit der Integrationsschrittweite von der Rechenzeit. Wenig überraschend sinkt die Rechenzeit bei Verwendung größere Zeitschrittweiten. Das Einschritt- und Mehrschrittverfahren hier so nah beieinander liegen, liegt daran, dass für diese Simulation nicht viel berechnet werden muss, der zusätzliche Rechenaufwand fällt also nicht stark ins Gewicht.

Bild 6: Um zu bestimmen, welches Verfahren bei größtmöglicher Genauigkeit am schnellsten rechnet wird hier der globale Fehler über der Rechenzeit aufgetragen. Fast jede der Kurven hat ein lokales Minimum des globalen Fehlers. Je genauer ein Verfahren ist, desto tiefer liegt sein Minimum. Das beste Verfahren ist dasjenige, das bei kleinstmöglichem Fehler am schnellsten rechnet. Interessanterweise liegen in diesem Fall ADB6 und RK5 gleichauf.

Wenn man herausfinden möchte, welches Verfahren die Lösung bei vorgegebener Genauigkeit am schnellsten errechnet, so muss man die entsprechenden Daten nur aus Bild 6 ablesen. Möchte man beispielsweise, dass die Quadratsumme des globalen Fehlers kleiner als 1e-5 ist, so ergibt sich folgende Tabelle:

Rang	Integrationsschema	Rechenzeit in ms	Zeitschrittweite
1	RK 5	0.01	0.02
2	RK 4	0.015	0.01
3	ADB 5	0.03	0.005
4	ADB 4	0.039	0.0035
5	ADB 3	0.09	0.0015
6	Euler mod. Heun	0.5	0.0003
7	RK3 ADB2	0.7	0.0003
9	Euler	36812	4e-9

Tabelle 2: Rangliste der Verfahren. Sortiert nach kürzest möglicher Zeit, in der die Berechnung mit einer Quadratsumme des absoluten Fehlers von ungefähr 1e-5, abgeschlossen wurde.

Der Sieg geht an das Runge-Kutta Verfahren 5. Ordnung (RK5)! Es ist in diesem Test überlegen, da es größere Zeitschrittweite erlaubt ohne viel an Genauigkeit einzubüßen. Ein starker zweiter Platz geht an das Runge-Kutta Verfahren 4. Ordnung (RK4), welches immer noch besser abschneidet als das Adams-Bashfort Verfahren 5. Ordnung (ADB5). Das ist insofern überraschend, als ADB5 als Mehrschrittverfahren deutlich weniger Funktionsauswertungen benötigt. Bei näherer Betrachtung wird aber klar, dass die Berechnungen für diese Pendelsimulation sehr einfach sind und nur minimalen Aufwand erfordern.

Vereinfacht gesagt können Mehrschrittverfahren ihre Vorteile erst dann ausspielen, wenn es etwas zu berechnen gibt. Die Ergebnisse wären für ein komplizierteres Problem (z.B. Dreikörperproblem) anders. Man sollte die Mehrschrittverfahren nicht auf Basis dieser einfachen Beispielrechnung abschreiben. Betrachtet man die anderen Verfahren, so fällt die enttäuschende Leistung von RK3 auf, das selbst schlechter als das modifizierte Euler Verfahren und das Verfahren von Heun abschneidet. Die Ursache hierfür liegt daran, dass es zwar mehr Funktionsauswertungen benötigt aber keine signifikant größeren Zeitschrittweiten zulässt.

Das magnetische Pendel

Der nächste Test wird sich mit dem magnetischen Pendel beschäftigen. Die physikalischen Prinzipien dazu werden im Video 1 erläutert. Das für die Simulation verwendete Modell ist in Bild 5 dargestellt. Die Simulation wird mit verschiedenen Integrationsverfahren durchgeführt. Die Ergebnisse werden dann kurz analysiert und besprochen.

Externer Inhalt: Chaos Theorie erklärt am Beispiel des Magnetischen Pendels / Aldo Cavini Benedetti (Youtube)

Bevor wir anfangen, sollten wir uns zwei Punkte der Simulation genauer ansehen. Die Pendelbewegung ist zwar chaotisch aber chaotisch bedeutet nicht, dass man sie nicht berechnen kann. Es bedeutet lediglich, dass der Rechenfehler exponentiell mit der Zeit anwächst. Man kann also nicht besonders weit in die Zukunft rechnen, weil früher oder später kleine Variationen in den Anfangsbedingungen anwachsen und letztendlich zu völlig unterschiedliche Ergebnissen führen werden.

Der erste Test wird die Spuren der verschiedenen Integrationsverfahren vergleichen. Alle Verfahren werden mit identischen Anfangsbedingungen initialisiert, so dass sämtliche Abweichungen nur durch die die Ungenauigkeiten der verschiedenen Integrationsverfahren verursacht werden sollten. Wie man in Bild 8 sehen kann, gibt es dabei einige Punkte, in denen es praktisch keinen Unterschied zwischen den verschiedenen Verfahren gibt, wohingegen für andere Startpunkte fast jedes Integrationsverfahren zu einem anderen Endpunkt konvergiert (Bild 9).

Bild 7: Das dem Test zugrunde liegende Pendelmodell.

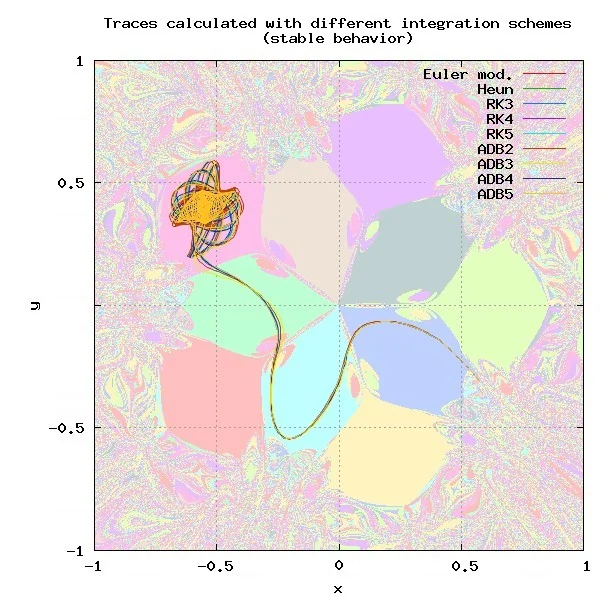Bild 8: Es gibt Startpunkte von denen aus alle Integrationsverfahren nahezu identische Ergebnisse liefern.

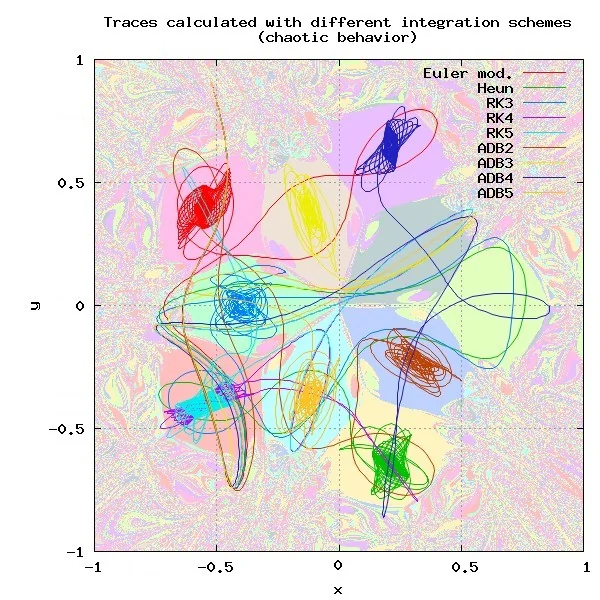Bild 9: Für andere Startpunkte liefern fast alle Integrationsverfahren unterschiedliche Ergebnisse.

Simulationsergebnisse

Vor diesem Hintergrund ist es nun interessant zu sehen, wie eine vollständige Berechnung aussieht. Folgende Bilder wurden mit einer Schrittweite von h=0.015 s berechnet:

Bild 10: Übersicht über die Ergebnisbilder der verschiedenen Integrationsverfahren.

Große Teile des Simulationsgebietes zeigen ein chaotisches Verhalten, der Mittelteil und einige Strukturen sind in allen Simulationen reproduzierbar. Die gute Nachricht ist: Alles sieht ziemlich ähnlich aus! Vielleicht sollten wir mal nachschauen, wie ähnlich genau:

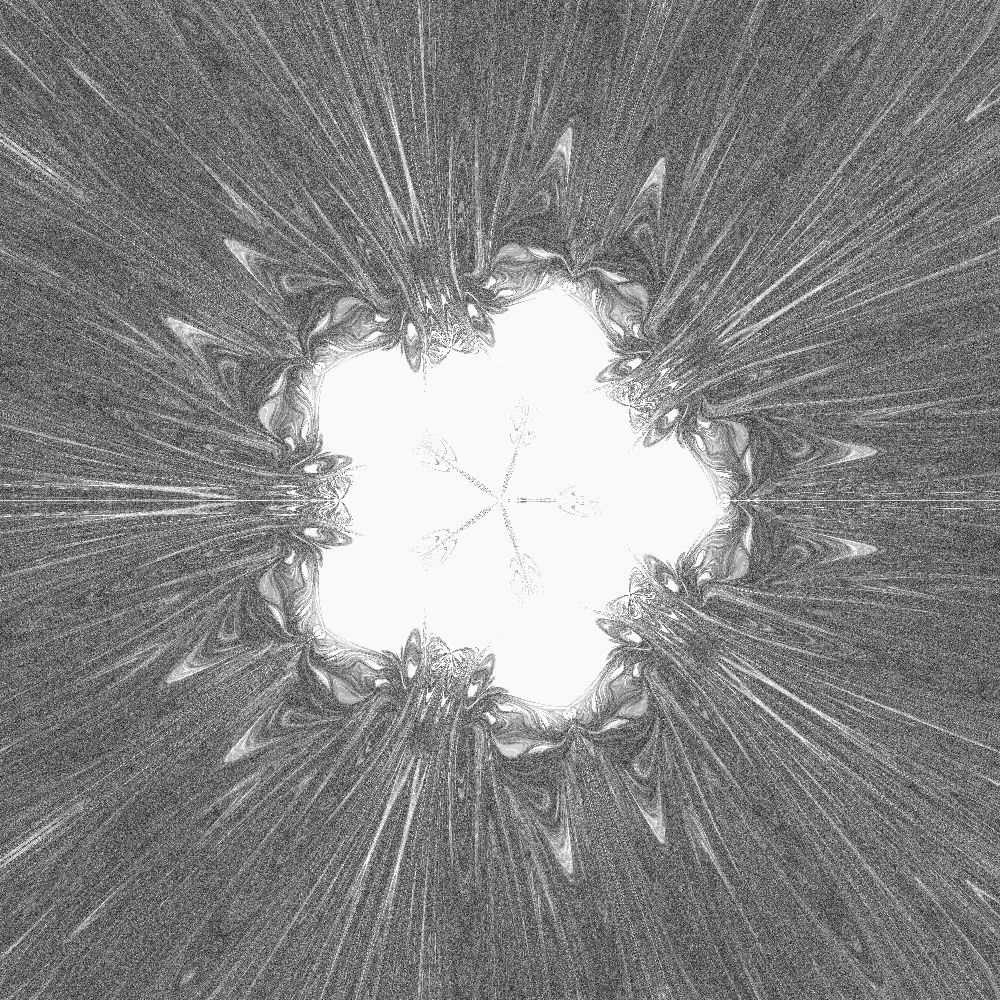Bild 11: Schwarzweißbild in dem der Wert eines Pixels angibt, wie viele verschiedene Ergebnisse die Integrationsverfahren lieferten. Weiß bedeutet alle Integrationsverfahren lieferten das gleiche Ergebnis, schwarz bedeutet alle lieferten ein anderes Ergebnis.

results filtered with differential image

Bild 12: Ergebnisbild, in dem Pixel nur angezeigt werden, wenn sie in mindestens 9 von 10 Integrationsverfahren gleiche Ergebnisse erzielt haben. Die Pixelfarben sind dem RK5 Verfahren entnommen.

Der weniger chaotische Zentralbereich der Simulation wird von allen Integrationsverfahren gut abgebildet. Im Außenbereich zeigt sich bei allen Verfahren die chaotische Natur des Problems. Da keine analytische Lösung des Problems vorliegt, kann man bei diesem Vergleich schwer sagen, welches Verfahren am genauesten rechnet. Es zeigt sich jedoch eine gute Übereinstimmung bei den Verfahren höherer Ordnung (RK4, RK5, ADB4, ADB5). Einzig das ADB3 Verfahren zeigt einige Unterschiede im Vergleich zu den anderen Lösungen.

Bei dem Ergebnis einer numerischen Simulation sollte man sich klar machen, dass man nie die exakte Lösung erhält, sondern immer nur eine Näherung. Die Genauigkeit hängt vom numerischen Verfahren, den Start-, Rand- und Nebenbedingungen ab. Selbst kleine Änderungen in den Startwerten können große Änderungen im Ergebnis verursachen! Monte Carlo Simulationen können hier helfen, die Qualität des Ergebnisses besser zu beurteilen.

Download

Der Quellcode zu diesem Artikel ist als Open Source auf Github verfügbar. Das Beispielprojekt ist in C++ geschrieben.

C++ Quellcode herunter laden