Rendering a Galaxy with the density wave theory

Spiral galaxy M51. The galaxy has a clearlyvisible spiral structure with an abundance of H II regions shining red due to the radiation releasedby newly born stars.

This article explains how to set up a realistically looking spiral galaxy using basic astronomical and physical principles. The scientific background is explained briefly but only to the extend required to understand the simulation. The article is accompanied by C++ and Typescript source code for the procedural generation of a 2d galaxy with SDL2 and OpenGL/webGL.

Spiral galaxies are amongst the most beautiful observable objects in the night sky. Take for instance the whirlpool galaxy shown in Image ?. The picture was taken with the NASA/ESA Hubble space telescope. It's one of my favorite images as it features all the components of a spiral galaxy in great detail. One can see a clear spiral structure with a lot of bright red H-II-regions. In addition the spiral arms show a fine pattern of darker lines which are formed by interstellar gas and dust clouds. The gas and dust clouds provide gas and heavy elements required to form new stars and planetary systems. The spiral arms are the places where new stars are born.

Pretty as it is, it's just an image. How might a rotating galaxy look like? To find out one might use N-Body simulations but they are quite complicated and require more computational time than desirable. What we need is a "shortcut", a way to spare ourself the complexity of calculating the interactions between thousands of stars without oversimplifying the problem. For this simulation the "shortcut" is the density wave theory. It will enable us to render a realistically looking galaxy without taking care of the complex n-body interactions involved in the real world.

Click here go build your own galaxy:

Density Wave theory

As early as 1925, the Swedish astronomer Bertil Lindblad recognized that our Milky Way was rotating. He also recognized that the angular velocity of this rotation is decreasing outwards. Therefore the spiral arms could not be a mere static accumulation of stars and dust. Due to the differential rotation of the Milky Way they would dissolve within a short time ("Winding Problem"; Animation 2). To solve this problem, he developed a first version of density wave theory. The basis is the assumption that in the gravitational field of a galaxy a density wave revolves at a constant speed. This angular velocity generally does not match the rotational speed of the rest of the system. In the mid 1960 Lindblad's ideas were further developed by the Chinese astronomers CC Lin and Frank Shu [1].

Originally, astronomers had the idea that the arms of a spiral galaxy were material. However, if this were the case, then the arms would become more and more tightly wound, since the matter nearer to the center of the galaxy rotates faster than the matter at the edge of the galaxy (see Animation 2). The arms would become indistinguishable from the rest of the galaxy after only a few orbits. This is called the winding problem [3]. Lin and Shu proposed in 1964 that the arms were not material in nature, but instead made up of areas of greater density, similar to a traffic jam on a highway [1]. As the cars move through the traffic jam, the density of cars increases in the middle of it. The traffic jam itself, however, does not move (or not a great deal, in comparison to the cars). In the galaxy, stars, gas, dust, and other components move through the density waves, are compressed, and then move out of them.

Classification of spiral galaxies

In order to classify spiral galaxies a classification scheme was devised by Edwin Hubble in 1936. This classification scheme is still in use today. Hubble distinguished between elliptical galaxies and spiral galaxies. The elliptical galaxies were rated based on their eccentricity and given identifiers ranging from E0 to E7 with the eccentricity increasing towards E7.

The type S0 is an intermediary form of galaxy that marks the transition to the spiral galaxies. Spiral galaxies were separated into two categories on their own. The spiral galaxies and (Sa bis Sc) and the barred spiral galaxies (SBa bis SBc).

Classification of galaxies according to Edwin Hubble; Courtesy of: Ville Koistinen (CC BY-SA 3.0)

For the rest of this article only spiral galaxies will matter. According to the classification scheme the following observations can be made for the different types of spiral galaxies:

• The spiral arm structure becomes more open from a to c
• The amount of dust and young stars decreases from a to c.
• The round central bulge of the galaxy decreases in size relative to the disc size from a to c.

Trajectories of the stars

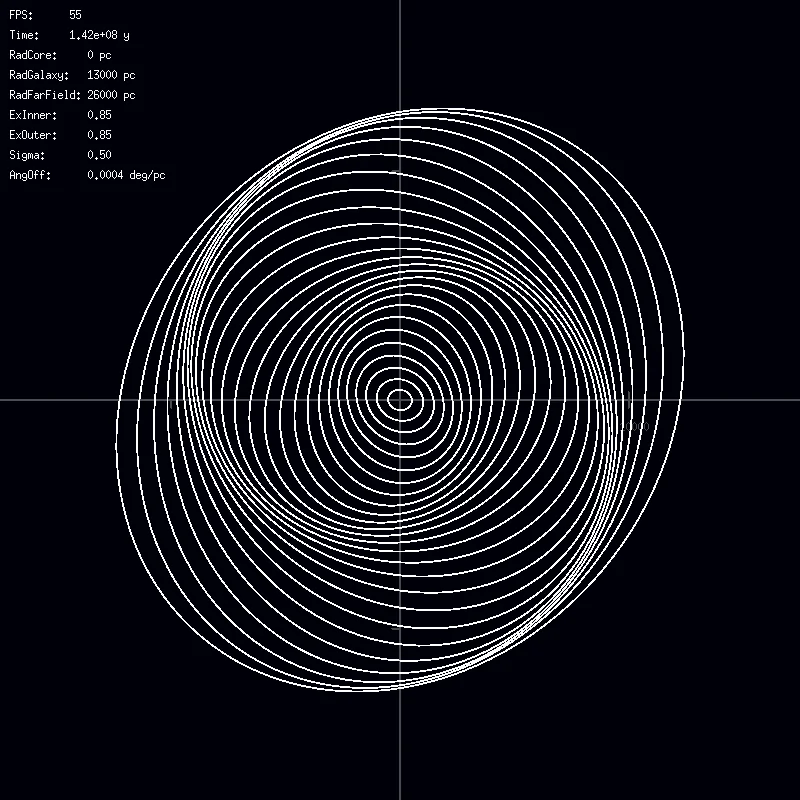A number of ellipsis slightly tilted against one another as their diameter is increasing.

Orbits of a galaxy similar to those predicted by the density wave theory. The bulge area is marked with yellow. The innermost spiral structure slightly resembles a bar. The green circle marks the edge of the galaxy.

The first problem of modeling a realistically looking galaxy is getting its shape right. One theory for explaining the spiral structure is the density wave theory. It explains the typical spiral arm structure as a result of regions with higher star density caused by slight variations in the orbits of its stars. These regions are not static. Stars will move in and out of them as they orbit the galaxy. The Spiral arms can be modeled by using elliptical orbits that are tilted slightly as their radii grow. Although this is a simplification of the orbits it will serve us well for getting a realistically looking shape of the galaxy. I will use the following simplified assumptions for the orbits in the galaxy:

• The orbits of the stars in the galaxy are ellipses. The galactic center is in the focal point. (1. Law of Kepler)
• Adjacent stars will roughly move into the same direction.
• The orbits are slightly tilted with increasing diameter.

To be clear: In reality orbits look different! They are not closed like an ellipses but open like a rosette. This difference however would not make a significant difference to the visual appearance of the galaxy. Taking Kepler's first law for approximating the orbits isn't very accurate either because the mass of a galaxy is not concentrated in its center but spread over the disk and bulge areas. However most mass is concentrated in the center so there is some justification for this assumption.

Bild ? shows elliptical orbits which exhibit a slight angular offset in their orientation as their diameter is increasing. Even this simple construction is clearly showing a spiral structure. The spiral arms start in the center of the galaxy and extend to the edge. There is no distinct bulge area visible.

Since observations show that most spiral galaxies have a distinct bulge area the visual model needs to be tweaked to represent this fact properly. The bulge area is often circular in shape and so the overall model should allow such shapes. For this reason the model is extended to always have a round core.

The eccentricities than increase towards the bulge-disk boundary (yellow circle in Bild ?) and from there they again change towards the edge of the galactic disk. Beyond the disc the eccentricities will again decrease until they reach circular shapes at twice the diameter of the galactic disc. This represents a galactic halo but only few stars will be rendered there in the simulation later. For simplicity Bild ? does omit these orbits as they don't contribute much to the overall shape of the galaxy.

Surface brightness distribution

Once the orbits are known the galaxy can be populated with stars. This section will provide some background information on the distribution of stars in a spiral galaxy. It will lead to a model allowing the distribution of the stars in a way similar to what is observable in real galaxies. The basic assumption is that stars should be distributed in such a way that the surface brightness distribution of a real galaxy is matched. The surface brightness distribution of the bulge is similar to those of an elliptical galaxy. It can be estimated using the de Vaucouleurs-law:

with \(I_0\) being the central intensity. According to Freeman [3] the surface brightness distribution of the galactic disc can be described using an exponential law:

with \(I_0\) being the Central intensity and \(R_D\) a characteristic scale length (Distance in which the intensity drops to 50%). The total surface brightness distribution can be obtained by combining both equations as shown in Bild ?. For the modeling of the galaxy it is assumed that the distribution function of the stars is similar to the surface brightness function. Applying such a distribution function to the density wave diagrams shown earlier yields the result shown in Bild ?. The image begins to look like a galaxy even though the stars are drawn as plain white dots.

Model of a galaxy featuring a star distribution that closely resembles the surface brightness distribution of observed galaxies

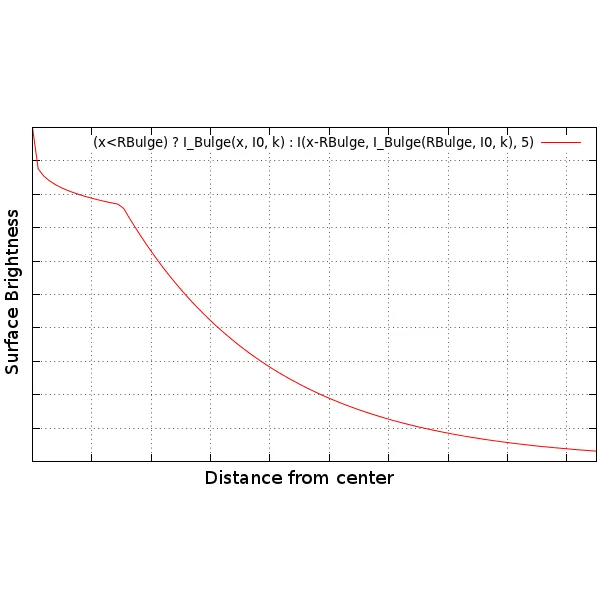Schematic surface brightness distribution of a spiral galaxy according to Freeman and de Vaucouleurs combined into a single diagram.

The color of stars

In the previous section the galaxy and its distribution of stars was discussed. For a realistic rendering it is crucial to apply a realistic coloring scheme as stars in a galaxy can only have specific colors. The color of a star greatly depends on its surface temperature. The underlying physical principle is the so called Black-body radiation.

Color temperature according to Planck's law of radiation.

A realistic color scheme should be restricted to colors which are plausible according to Planck's law. For the rendering model the surface temperature of the stars in the simulated galaxy lies between 3000 and 9000 Kelvin. In reality the surface temperature of a star will be subject to change throughout its lifespan as it progresses in its path in the so called Hertzsprung Russell diagram.

Calculating the color based on a given temperature is a pretty complex process which I won't discuss here in detail. Instead I will use a program called specrend.c which was written by John Walker [5]. For those interested in the physical background of his program i recommend reading his web site where he explains the algorithm in depth. For all others it will suffice to say that his program computes the RGB values for a given temperature.

Image ? shows the result of applying coloring based on Planck's law to the galaxy shown in Image ?. The exponential increase in star density towards the center is now better visible as star colors differ. However the galaxy as a whole still appears to be consisting of a number of more or less unrelated points. At this point the simulation is already rendered by using approximately 60000 stars. Simply rendering more stars doesn't appear to be viable option due to performance constraints.

In reality galaxies consist of billions of stars. Simply rendering more stars won't do the trick. Even in a photographic image of a spiral galaxy, the resolution isn't high enough to display distinct stars (unless they are extraordinary bright). What is visible in images is a kind of nebulae which would turn into distinct stars only if you would be able to zoom in greatly. For this reason the model needs an additional feature representing all those stars which are to small to be seen separately. In addition to the stars, nebulae will be added to the galaxy. When using OpenGL one can use the point sprite extension to get the desired effect. For simplicity the nebulae will be distributed evenly over the galactic disc. The result is shown in Image ?.

A rendered galaxy with colors based on the color temperature predicted by a simple black-body model.

Galaxy with stars and nebulae based on OpenGL point sprites. The spiral structure is now more prominent.

The final result shows a galaxy with stars, nebulae and H-II regions concentrated in the spiral arms of the galaxy.

Image ? is already a pretty good approximation of the galaxy but one crucial thing is still missing: H-II regions. If you look carefully at Bild ? you will see an abundance of bright red nebulae distributed across the spiral arms. These nebulae are so called H-II regions, huge intergalactic clouds composed of hydrogen. They are galactic nurseries full of newly born bright hot stars whose emissions make the surrounding hydrogen glow in a characteristic red color.

To match the appearance of a real galaxy, the model also needs H-II regions and they should be located in the spiral arms just like in reality. This will be achieved with a trick, first H-II regions are evenly distributed amongst the galactic disc much like ordinary stars except they are rendered as red nebulae. But in order to restrain their visibility to the spiral arms their rendering size is proportional to the distance of two adjacent density waves with a cutoff size below a certain threshold. As a result they only appear in the spiral arms but move exactly like ordinary stars.

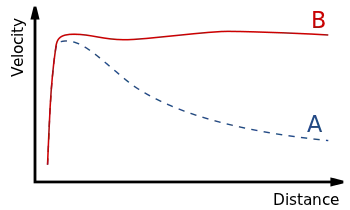Rotational curve of a galaxy

Rotational curve of a galaxy. Image courtesy of Phil Hibbs (CC BY-SA 3.0) Animation 4: The final result of the simulation shows a galaxy with H-II regions spinning in a manner similar to real galaxies. (own work; CC BY 4.0)

Until now the motion of the galaxy was ignored. This section will finally discuss the motion of a galaxy. Therefore lets look at a galaxies rotation curve. A rotation curve shows how fast the stars and gas components of a galaxy move as a function of their distance from the galactic center. Observations show that the inner part of a galaxy is almost moving like a rigid body. This is causing a steep linear ascent in the rotation curve close to the galactic center. With increasing distance from the center the rotation curve flattens and is almost becoming a constant (Image ?; curve B).

Interestingly enough this is a contradiction to models based on the distribution of the visible mass of a galaxy (Image ?; Curve A) that led to the hypothesis of the existence of dark matter. Dark matter is an unknown kind of matter that does not interact with visible matter in any form except by its gravitational force. So its not just dark, it's invisible, virtually undetectable except through its gravitational force. It is in fact so mysterious that various attempts have been made to get rid of the concept of dark matter altogether and explain it's effects by tweaking the law of gravity but so far dark matter is still the most accepted explanation for the observed rotation curves of galaxies.

The only thing left to do is to make sure that the rotation curve is similar to the one displayed in Image ?. The final result is shown in Animation 4. It features a galaxy with two spiral arms and H-II regions. The galaxy is of hubble type Sb.

Download

C++ and Typescript source code with implementations of this algorithm are available for download via GitHub.

Download Galaxy Renderer (C++ Version)

Download Galaxy Renderer (Typescript Version)

References

1. C.C. Lin, Yuan, C., and F.H. Shu, "On the Spiral Structure of Disk Galaxies III. Comparison with Observations", Ap.J. 155, 721 (1969). (SCI)
2. Carroll, Bradley W. and Dale A. Ostlie, "An Introduction to Modern Astrophysics." (2007). Addison Wesley. pp. 966.
3. Freeman, K. C., "On the Disks of Spiral and S0 Galaxies" (1970). Astrophysical Journal, vol. 160, p.811
4. Density wave theory. In Wikipedia, the free encyclopedia. Retrieved May 05, 2020, from https://en.wikipedia.org/wiki/Density_wave_theory
5. John Walker "Colour Rendering of Spectra." (1996, April 25). Webpage, retrieved from http://www.fourmilab.ch/documents/specrend/