The Chaos Game

Various fractal patterns created by the Chaos Game

The first 7 steps of the chaos game for the corner points ACABBCB.

The complete Sierpinski Triangle

What is the Chaos Game?

Fractals are self-similar patterns. The so-called chaos game (also called a random iteration algorithm) is a method to generate iterative fractals with the help of polygons.

The rules are simple and will be explained using the example of a triangle. It has the corner points A, B and C. You start the chaos game at a random point P1 within the triangle. To calculate the next position P2, you choose one of the three corner points of the triangle at random and place P2 in the middle of the route between point P1 and the randomly selected corner point. You repeat this process as often as you like and draw every point you obtain on to the screen.

It is striking that some areas of the triangle cannot be reached in later steps. These areas form a fractal pattern. Only the first steps (orange in the picture) can land in these areas, all other points (green in the picture) land in between.

The result is a fractal, the so-called Sierpinski triangle. It was first described by the Polish mathematician Wacław Sierpiński in 1915. But it already appears in floor patterns in medieval Rome. [2].

Generalization to arbitrary polygons

This construction mechanism for fractals can be applied to any polygon. However, if you increase the number of corners, you should no longer halve the distance, but adjust the factor slightly, otherwise the algorithm will not always create a fractal. For example: If you halve the distance between the current position and the randomly selected corner of a square you get an evenly filled area and not a fractal.

Halving the distance in a triangle corresponds to multiplying its length by a factor of 0.5. If this is generalized to polygons with n-vertices, then a favorable factor for any polygons with n-corner points can be computed with this equation [1]:

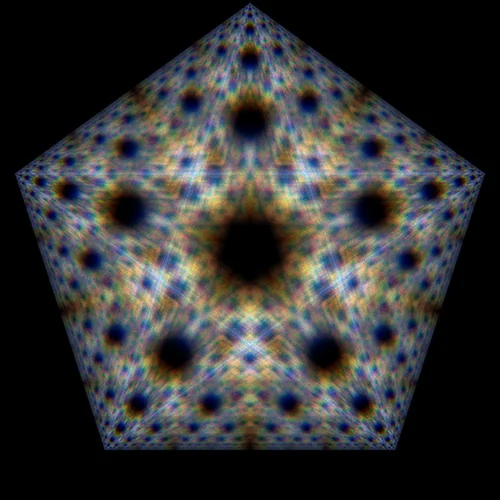
The results of runs of the chaos game for polygons with 3, 4 and 5 corners are shown in the following images. In addition a different color was assigned to each corner point of the polygon. The color is assigned based on the the position of a corner point in the color wheel. During the calculation, each new point is colored with the color of the corner point in the direction in which it last jumped.

Constraining the random selection of corner points

So far, the fractals look kind of regular. To change that, another modification is introduced. The corner points are still randomly selected, but constraints on the selection are introduced. Such constraints can include:

• A corner point must not be selected twice in succession
• If a corner point has been selected, none of its neighbors may be selected in the next step.
• If the same corner point was selected twice in succession, the corner point selected in the next step must at least be 2 corners away.

Imagination knows no bounds. The following things can now be changed in our version of the random iteration algorithm:

• The number of corner points of the base polygon
• The factor r, which determines how far a point jumps in an iteration step in the direction of the randomly selected corner point
• Additional rules that slightly limit the "randomness" of the corner selection

n=5, r=0.5; Random corner point selection

n=5, r=0.5; Cornerpoints cannot be choosen twice in a row

n=5, r=0.5; If a cornerpoint is chosen twice, the next selected point must not be a direct neighbor.

An alternate method of coloring

An alternative method of coloring is to run the chaos game with slightly changed parameters for each color channel (red, green and blue) separately. With this approach, no color is assigned to the corner points of the polygon. Pixels on the screen are increased in brightness when the chaos game lands on a pixel. Only the brightness of the color channel assigned to the respective chaos game is increased.

That alone would not be enough, because three identical chaos games on three color channels would only produce a grayscale image. In order to bring more color into the simulation, the parameters of the three chaos games have to differ slightly. This can be achieved by modifying the parameter r for each of the chaos games minimally and randomly. The following three pictures show the result of such a modification.

n=5, r=0.5; Random corner point selection

n=5, r=0.5; Cornerpoints cannot be choosen twice in a row

n=5, r=0.5; If a cornerpoint is chosen twice, the next selected point must not be a direct neighbor.

Explaining the source code

The implementation of the random iteration algorithm described here can be implemented in less than 80 lines of Python source code.

import pygame
import random
import math
import colorsys
from pygame.locals import *

idx = [0, 0, 0]

def mark_pixel(surface, pos, pcol):
    col = surface.get_at(pos)
    surface.set_at(pos, (min(col[0] + pcol[0]/10, 255),
                         min(col[1] + pcol[1]/10, 255),
                         min(col[2] + pcol[2]/10, 255)))

def random_point_index(p):
    if len(p) <= 3:
        return random.randint(0, len(p) - 1)

    global idx
    idx[2] = idx[1]
    idx[1] = idx[0]
    dst1 = abs(idx[1] - idx[2])

    while True:
        idx[0] = random.randint(0, len(p) - 1)
        dst = abs(idx[0] - idx[1])
        if dst1 == 0 and (dst == 1 or dst == len(p) - 1):
            continue
        else:
            break

    return idx[0]

def init_polygon(width, height, n):
    delta_angle = 360/n
    r = width/2 - 10
    p = []

    for i in range(0, n):
        angle = (180 + i*delta_angle) * math.pi / 180
        color = colorsys.hsv_to_rgb((i*delta_angle)/360, 0.8, 1)
        p.append(((width/2 + r*math.sin(angle),
                   height/2 + r*math.cos(angle)),
                  (int(color[0]*255), int(color[1]*255), int(color[2]*255))))

    return p

def main(width, height, n, r):
    pygame.init()
    surface = pygame.display.set_mode((width, height))
    pygame.display.set_caption('Das Chaos Spiel')

    p = init_polygon(width, height, n)

    x, y = (400, 300)
    step = 0
    while True:
        step = step + 1
        point_idx = random_point_index(p)

        pos = p[point_idx][0]
        color = p[point_idx][1]
        x += (pos[0] - x) * r
        y += (pos[1] - y) * r

        mark_pixel(surface, (int(x), int(y)), color)

        if step % 1000 == 0:
            pygame.display.update()

        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.image.save(surface, 'chaosspiel.jpg')
                pygame.quit()
                return

if __name__ == "__main__":
    n=5; main(800, 800, n,  0.45)

This Python script uses the libraries random, math, colorsys and pygame . The pygame library must be installed via Python's package manager PIP before the program can be run. After the import instructions, the global variable idx is declared. This is a field in which the index of the last two selected polygon corner points are saved. This information is necessary to limit the random selection of corner points.

import pygame
import random
import math
import colorsys
from pygame.locals import *

idx = [0, 0, 0]

The function mark_pixel determines the color of the current pixel in the chaos game. The color is not set statically. If the position in the chaos game falls on a pixel, it is made a little lighter each time and colored in the color of the corner point that was chosen to get to this position. This results in beautiful color transitions in the fractal. Pixels that are not often visited are displayed darker.

def mark_pixel(surface, pos, pcol):
    col = surface.get_at(pos)
    surface.set_at(pos, (min(col[0] + pcol[0]/10, 255),
                         min(col[1] + pcol[1]/10, 255),
                         min(col[2] + pcol[2]/10, 255)))

The function random_point_index selects a random corner point of the polygon and returns its index. For this purpose, it receives an array of polygon corner points as its input parameter. For a purely random selection of points, it would be sufficient to use the bold line. The variant shown here contains the contraint that if the same corner point was selected twice, the next corner point must not be a direct neighbor.

def random_point_index(p):
    if len(p) <= 3:
        return random.randint(0, len(p) - 1)

    global idx
    idx[2] = idx[1]
    idx[1] = idx[0]
    dst1 = abs(idx[1] - idx[2])

    while True:
        idx[0] = random.randint(0, len(p) - 1)
        dst = abs(idx[0] - idx[1])
        if dst1 == 0 and (dst == 1 or dst == len(p) - 1):
            continue
        else:
            break

    return idx[0]

The init_polygon function initializes the corner points of the polygon. The input parameters include the size of the playing field and the number of polygon corner points. At the same time, a color is assigned to each of the corner points of the polygon. This color corresponds to the position of the point in the color wheel.

def init_polygon(width, height, n):
    delta_angle = 360/n
    r = width/2 - 10
    p = []

    for i in range(0, n):
        angle = (180 + i*delta_angle) * math.pi / 180
        color = colorsys.hsv_to_rgb((i*delta_angle)/360, 0.8, 1)
        p.append(((width/2 + r*math.sin(angle),
                   height/2 + r*math.cos(angle)),
                  (int(color[0]*255), int(color[1]*255), int(color[2]*255))))

    return p

The main function is the main loop of the program. The function receives the size of the playing field, the number of polygon corner points and a factor r that controls the jump length as its parameters. Then the graphic subsystem is initialized and the iterations are carried out. During the iterations the current position is saved in the variables x and y. Finally the image is saved after a certain number of iterations.

def main(width, height, n, r):
    pygame.init()
    surface = pygame.display.set_mode((width, height))
    pygame.display.set_caption('Das Chaos Spiel')

    p = init_polygon(width, height, n)

    x, y = (400, 300)
    step = 0
    while True:
        step = step + 1
        point_idx = random_point_index(p)

        pos = p[point_idx][0]
        color = p[point_idx][1]
        x += (pos[0] - x) * r
        y += (pos[1] - y) * r

        mark_pixel(surface, (int(x), int(y)), color)

        if step % 1000 == 0:
            pygame.display.update()

        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.image.save(surface, 'chaosspiel.jpg')
                pygame.quit()
                return

if __name__ == "__main__":
    n=5; main(800, 800, n,  0.45)

Weblinks

The YouTube channel Numberphile has published a video with further explanations of the Chaos Game. Among other things, it also deals with the Barnsley fern, a fractal that cannot be explained in more detail here.

References

1. Steffen Polster, "Chaosspiel - Mathematik alpha." auf https://mathematikalpha.de, accessed on 2020-05-03
2. Conversano Elisa, Tedeschini Lalli Laura (2011)"Sierpinski Triangles in Stone, on medival floors in Rome." APLIMAT Journal of Applied Mathematics, 4: 114, 122