Dithering und die Gutwerdung der Computergrafik

Dieses Bild verwendet insgesamt nur 8 Farben. Durch Dithering wird der Eindruck einer größeren Farbtiefe erzeugt. Für die Darstellung im Browser wurde eine leichte Unschärfe hinzugefügt um den Moiré-Effekt zu vermeiden. Das ist ähnlich wie bei der Darstellung auf normalen Fernsehgeräten, deren Schärfe ebenfalls beschränkt war. Tatsächlich sahen Computerspiele auf Fernsehern immer besser aus als auf hochauflösenden Monitoren.

Die Anfänge der modernen Computergrafik

Bereits die Impressionisten spielten mit der Erzeugung von Farben durch benachbarte farbige Punkte. Hier zu sehen im Bild "Antibes. Kleiner Hafen von Bacon.". Es ist ein pointilistisches Gemälde von Paul Signac aus dem Jahr 1917. (orig. Titel: "Antibes. Petit Port de Bacon"; via Wikimedia Commons; gemeinfrei)

Zu Beginn der 80er Jahre des letzten Jahrhunderts traten die Heimcomputer ihren Siegeszug in den Wohnzimmern der Welt an. Ihre grafischen Fähigkeiten waren hinsichtlich Bildschirmauflösung und Farbpalette beschränkt. Dies stellte Entwickler und Grafikdesigner vor Herausforderungen, ihre kreativen Vorstellungen auf dieser beschränkten Hardware zu realisieren. Wie stellt man einen eindrucksvollen Sonnenuntergang mit lediglich 2, 4 oder 16 Farben dar?

Die Antwort ist Dithering, auch Fehlerdiffusion genannt. Dabei handelt es sich um eine Bildbearbeitungstechnik, bei der durch geschicktes Platzieren farbiger Pixel die Illusion einer größeren Farbtiefe erzeugt wird. Diese Technik haben sich die Computergrafiker von den französischen Impressionisten abgeschaut. Diese hatten bereits herausgefunden, wie man durch das Platzieren kleiner Farbflecken in unmittelbarer Nachbarschaft die Illusion einer anderen Farbe erzeugen konnte. Eine Zeichentechnik, die zunächst abwertend "Pointillismus" genannt wurde.

Einhundert Jahre später, in den 80er Jahren des 20. Jahrhunderts, wurde die Technik wieder bzw. neu entdeckt. Jetzt gab es durch die begrenzten Grafikfähigkeiten der Heimcomputer neue Anwendungsfälle und durch das Ankommen von Computerspielen im Mainstream auch einen Markt dafür.

"The Secret of Monkey Island" (1990) von Lucasfilm Games. Die Bildschirmgrafik der 16 farbigen PC-EGA Version zeigt im Himmel die typischen Muster eines geordneten Ditherings.

Heute hat sich der Kreis geschlossen. Dithering ist wieder ein künstlerisches Gestaltungselement geworden. Man erreicht damit den 8-bit Retro Look in modernen Computerspielen oder generiert neue Computerspiele mit ganz eigener Ästhetik wie beispielsweise in "Return of the Obra Dinn". Für bessere Computergrafik braucht man es heute nicht mehr, denn bei modernen Grafikkarten gibt es schon lange keine wahrnehmbaren Darstellungslimits mehr.

Grundlagen der Farbreduktion

Das Problem der Farbreduktion soll an einem Beispiel erläutert werden. Wir gehen von einem digitalisierten Bild aus, das bis zu 16777216 mögliche Farben enthalten kann. Dieser Wert ergibt sich daraus, dass die Farbinformation von Bildern im Jpeg-Format in den drei Farbkanälen Rot, Grün und Blau gespeichert wird. Jeder Farbkanal kann 256 verschiedene Helligkeitswerte annehmen. Das ergibt insgesamt 256 * 256 * 256 = 16777216 verschiedene mögliche Farben. Wir wollen das Bild für die Darstellung auf einem monochromen Monitor optimieren. Dieser Monitor kann nur schwarze und weiße Bildpunkte darstellen.

Im ersten Schritt wandeln wir das Bild in Graustufen um. Mit Hilfe eines Schwellwertalgorithmus erzeugen wir daraus ein Schwarzweißbild. Dieser Algorithmus vergleicht die Helligkeit jedes Pixels des Graustufenbildes mit einem Schwellwert und macht es weiß, wenn es über dem Schwellwert liegt, oder schwarz, wenn es darunter liegt.

Wir beginnen mit einen Graustufenbild. Dieses Bild hat 8 bit Farbtiefe, was sich in 256 verschiedenen Helligkeitsstufen pro Pixel ausdrückt.

Schwellwertalgorithmen sind nicht geeignet, Bilder in Schwarzweißbilder umzuwandeln, da lokale Helligkeitsinformationen fast vollständig verloren gehen.

Das Ergebnis ist enttäuschend. Das Bild ist kaum erkennbar. Es zeigt große einfarbige Bereiche, in denen jegliche Details fehlen (sog. "Banding"). Man könnte versuchen, den Schwellwert zu verändern, aber das würde nicht viel helfen. Lokale Bildinformationen gehen komplett verloren, wenn der Kontrast zu gering ist.

Geordnetes Dithering mit Bayer-Matrizen

Mit 2x2 Bayer-Matrix ergeben sich 4 verschiedene Muster für einen Helligkeitsgradienten.
Mit 4x4 Bayer-Matrix ergeben sich 16 verschiedene Muster.
Mit 8x8 Bayer-Matrix ergeben sich 64 verschiedene Muster.
Schwellwertkarte aus Basis einer 8x8 Bayer-Matrix, welche gekachelt wurde. Das rote Quadrat markiert eine Zelle.

Geordnetes Dithering ist eine Verbesserung des einfachen Schwellwertalgorithmus. Es basiert auf einem Schwellwertabgleich mit einer Schwellenwertkarte, die aus einer vordefinierten Matrix erstellt wird. Diese Matrix wird Bayer-Matrix genannt. Die Bayer-Matrix kann in verschiedenen Größen berechnet werden. Je größer die Matrix, um so mehr Helligkeitsabstufungen kann sie abbilden.

Für Bilder mit 8 Bit Farbtiefe müssen die Matrizen noch mit 256 multipliziert werden. Die 2x2 Bayer-Matrix mit den Schwellwerten für 8 Bit lautet also:

Die Schwellwertkarte wird erstellt, indem die Bayer-Matrix in x und y solange gekachelt wird, bis sie die gleiche Auflösung, wie das farbzureduzierende Bild hat. Für das Dithering wird nun jedes Pixel des Originalbildes mit dem Wert der Schwellwertkarte verglichen. Ist er größer, wird das Pixel weiß, ist er kleiner, wird das Pixel schwarz. [3]

Das Dithering mit einer Matrixgröße von 2x2 überzeugt nicht. Vier Muster für die Graustufendarstellung sind zu wenig, allerdings ist das Motiv jetzt erkennbar. Das Bild mit 8x8 Matrixgröße ist besser und sieht ganz okay aus. Es zeigt sich jedoch, dass diese Art des Ditherings störende, sich wiederholende Muster erzeugt.

Geordnetes Dithering mit 2x2 Bayer-Matrix. Die Qualität überzeugt nicht. Banding ist immer noch sichtbar, jetzt jedoch mit monochromen Mustern.

Geordnetes Dithering mit 8x8 Bayer-Matrix. Das Motiv wird deutlicher abgebildet aber es entstehen störende, regelmäßige Muster.

Dithering mit Bayer-Matrizen wird heute noch gelegentlich eingesetzt aber es gibt bessere Methoden. Auch wenn die Ergebnisse nicht berauschend sind, so ist ein entscheidender Vorteil dieser Methode ihre Einfachheit. Algorithmisch eignet sie sich beispielsweise sehr gut für die Umsetzung auf den Shadern moderner Grafikkarten.

Dithering mit zufälligem Rauschen

Beim Dithering mit Bayer-Matrizen werden Graustufen durch Helligkeitsvergleich mit einer Schwellwertkarte in schwarze und weiße Pixel umgewandelt. Die Schwellwertkarten wurden durch Kachelung der Bayer-Matrizen erzeugt. Dies führte zu störenden, sich wiederholenden Mustern im fertigen Bild.

Was liegt also näher als die Schwellwertkarten zu "verzufälligen" um diese Muster zu beseitigen? Nicht umsonst leitet sich der Begriff Dithering vom englischen Wort für "zittern" ab. Für eine einfache Implementierung in Python vergleicht man jedes Pixel des Ausgangsbildes mit einem zufällig gewählten Helligkeitswert. Ist der Helligkeitswert des Pixels größer, wird es weiß, ist er kleiner, wird es schwarz.

Dithering mit normalverteilten Zufallszahlen. Aus Gründen der Vergleichbarkeit wurde die gleiche Auflösung verwendet wie bei den Beispielen mit den Bayer-Matrizen.

def dither_noise(gray_img):
    height, width = gray_img.shape

    for y in range(height):
        for x in range(width):
            old_pixel = gray_img[y, x]
            new_pixel = 0 if old_pixel < random.randint(0, 255) else 255
#            new_pixel = 0 if old_pixel < int(np.random.normal(127, 64)) else 255
            gray_img[y, x] = new_pixel

    return gray_img

Es ist sinnvoll 127 als Schwellwert beizubehalten, weil dies der Mittelwert der Helligkeitsskala ist. Man kann verschiedene Verteilungen von Zufallszahlen probieren aber das Ergebnis wird sich qualitativ nicht dramatisch ändern. Man kann das Schiff erkennen aber das Ergebnis ist ziemlich stark verrauscht. Man kann mit dieser Art des Ditherings durchaus interessante Effekte erzielen, wenn die Auflösung das Ausgangsbildes groß genug ist. Praktische relevanz hat diese Method jedoch nicht.

Fehlerdiffusionsalgorithmen

Eindimensionale Fehlerverteilung

Für eine Verbesserung der Ergebnisse sehen wir uns nun Algorithmen an, die den Quantisierungsfehler berücksichtigen und diesen auf benachtbarte Pixel verteilen. Schauen wir uns zunächst einen einfachen Helligkeitsverlauf an, der mittels eines Schwellwertalgorithmus auf nur zwei Farben reduziert werden soll.

Ein Helligkeitsverlauf von dunkel zu hell über 10 Pixel.

Nach Anwendung des Schwellwertfilters werden die ersten 7 Pixel schwarz, weil deren Werte kleiner als 127 sind, die restlichen drei Pixel werden weiß. Die Summe des Quantisierungsfehlers über alle 10 Pixel beträgt -200. Dieser Wert fehlt in der Gesamthelligkeit der Pixelfolge. Für ein besseres Ergebnis benötigt man einen Algorithmus, der den Quantisierungsfehler berücksichtigt und ausgleicht.

Anwendung eines Schwellwertfilters mit dem Schwellwert 127. Das erste Pixel hat die Helligkeit 12, wird aber auf 0 gesetzt. Der Quantisierungsfehler dieses Pixels beträgt also -12. Sie Summe des Quantisierungsfehlers über alle Pixel beträgt 200.

Ein einfacher Algorithmus zur Fehlerdiffusion ist es, den Quantisierungsfehler auf das nächstgelegene Pixel zu übertragen. Bei Bearbeitung von links nach rechts wird er also dem rechten Nachbarn zugeschlagen. Dieser neue Wert wird dann mit dem Schwellwert verglichen und bearbeitet.

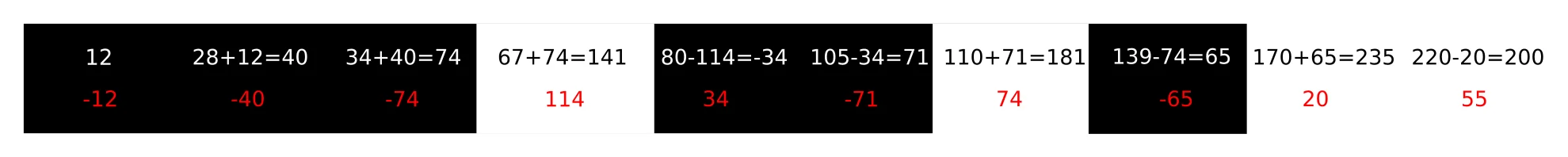Übertragung des Quantisierungsfehlers auf das rechte Nachbarpixel.

Wendet man diesen einfachen Fehlerdiffusionsalgorithmus auf das Beispielbild an, so sieht das Ergebnis wie unten dargestellt aus. Sagen wir einfach, dass es nicht komplett furchtbar ist. Das Schiff ist erkennbar aber es gibt deutliche Artefakte. Fehlerdiffusion findet hier nur in X-Richtung statt und bei ähnlichen Farbverläufen in den Zeilen werden auch die Ausgleichspixel für die Fehlerkorrektur an ähnlichen Stellen gesetzt. Im Ergebnis zeigen sich deutliche vertikale Linienstrukturen.

Einfacher Ditheringalgorithmus mit Fehlerdiffusion ausschliesslich in X-Richtung.

Eine naheliegende Verbesserung ist die Verteilung des Quantisierungsfehlers in 2 Dimensionen anstelle von nur einer.

Zweidimensionale Fehlerverteilung

Der Floyd-Steinberg-Algorithmus verteilt den Quantisierungsfehler mit unterschiedlicher Wichtung auf benachbarte Pixel. Dunkelgraue Pixel sind die Teile des Bildes, die bereits bearbeitet wurden. Die dunkelblaue Zelle ist die aktuelle Zelle und die blassblauen Zellen sind die Nachbarzellen, auf die der Quantisierungsfehler verteilt wird.

Floyd-Steinberg-Algorithmus

Der bekannteste Fehlerdiffusionsalgorithmus ist der von Robert Floyd und Louis Steinberg im Jahr 1976 veröffentlichte Floyd-Steinberg-Algorithmus. Er und alle anderen hier beschriebenen Algorithmen bearbeiten ein Bild durch Iteration über alle Zeilen und Spalten. Jedes Pixel wird dabei nur einmal besucht. Die Fehlerdiffusion erfolgt immer nur in Vorwärtsrichtung der Zeilen bzw. Spalten. Quantisierungsfehler können nur auf noch nicht besuchte Zellen übertragen werden.

Der Algorithmus verwendet für die Fehlerdiffusion nur die vier noch nicht besuchten, direkten Nachbarzellen. Dadurch ist er relativ schnell und kann so ohne Zwischenspeicher das komplette Bild in einem einzigen Durchlauf abarbeiten. Die bereits verarbeiteten Pixel werden nicht verändert, während die noch zu verarbeitenden Pixel entsprechend den auftretenden Quantisierungsfehlern modifiziert werden.

Der folgende Quellcode zeigt ein Implementierung des Floyd-Steinberg-Algorithmus in Python.

def __dither_core_floyd_steinberg(gray_img):
	height, width = gray_img.shape

	for y in range(height):
		for x in range(width):
			old_pixel = gray_img[y, x]
			new_pixel = 255 if old_pixel > 127 else 0
			gray_img[y, x] = new_pixel
			error = old_pixel - new_pixel

			# Distribute the quantization error to the neighboring pixels, with rounding
			if x + 1 < width:
				gray_img[y, x + 1] = min(255, max(0, gray_img[y, x + 1] + int(error * 7 / 16)))
			if x - 1 >= 0 and y + 1 < height:
				gray_img[y + 1, x - 1] = min(255, max(0, gray_img[y + 1, x - 1] + int(error * 3 / 16)))
			if y + 1 < height:
				gray_img[y + 1, x] = min(255, max(0, gray_img[y + 1, x] + int(error * 5 / 16)))
			if x + 1 < width and y + 1 < height:
				gray_img[y + 1, x + 1] = min(255, max(0, gray_img[y + 1, x + 1] + int(error * 1 / 16)))

	return gray_img

Der Floyd Steinberg Algorithmus erzeugt kurze, schlierenförmige Artefakte, die jedoch nur selten störend wirken, ihm aber ein characteristisches Aussehen geben. Daher wurden für eine qualitativ bessere Farbreduktion bald weitere Algorithmen entwickelt, die den Quantisierungsfehler auf mehr als nur die direkten Nachbarzellen verteilen.

Weitere Fehlerverteilungs-Algorithmen und deren Implementierung

In den Jahren nach 1980 wurden schnell eine Vielzahl weiterer Algorithmen von verschiedenen Autoren vorgeschlagen. Für die Heimcomputer kamen diese zu spät oder waren zu rechenintensiv. Dithering nach Floyd-Steinberg und selbst mir Bayer-Matrizen war gut genug. Zum Anderen lösten in den 1990er Jahren PC's die Heimcomputer ab. Deren VGA-Grafikkarten konnte nun 256 Farben aus 262144 gleichzeitig darstellen. Mit mehr Farben waren auch die Qualitätsunterschiede zwischen den verschiedenen Dithering-Methoden weniger wichtig. Eine Zeit lang fand Dithering noch Anwendung bei der Erstellung von Grafiken für Webseiten, da man durch Farbreduktion auch das Datenvolumen der Bilder verringern konnte.

Atkinson-Algorithmus

Stucki-Algorithmus

Sierra-Algorithmus

Erwähnenswerte Algorithmen sind der Atkinson-Algorithmus, der von Bill Atkinson, einem Softwareingenieur von Apple entwickelt wurde und in diesem Ökosystem breite Anwendung fand. Die Algorithmen von Peter Stucki und der Sierra-Algorithmus von Frankie Sierra dürften zu den qualitativ besten Dither-Algorithmen gehören.

Floyd-Steinberg-Algorithmus

Atkinson-Algorithmus

Sierra-Algorithmus

Stucki-Algorithmus

Diese Algorithmen kann man so implementieren, dass die Ditheringfunktion einen allgemeinen Fehlerverteilungskernel als Matrix übernimmt. Für Floyd-Steinberg Dithering würde der Aufruf einer solchen Funktion wie folgt aussehen:

kernel = np.array( [[0,  0,    0,   7/16, 0],
					[0, 3/16, 5/16, 1/16, 0],
					[0,  0,    0,    0,   0]] )
output = DitherProcessor.__dither_diffusion_generic_core(image, kernel)

Die Ditheringfunktion übernimmt den Kernel und verteilt die Fehlerwerte entsprechend der Kernelwerte auf die Nachbarpixel.

def __dither_diffusion_generic_core(gray_img, kernel):
	height, width = gray_img.shape

	for y in range(height):
		for x in range(width):
			old_pixel = gray_img[y, x]
			new_pixel = 255 if old_pixel > 127 else 0
			gray_img[y, x] = new_pixel
			quant_error = old_pixel - new_pixel

			# Distribute the quantization error to the neighboring pixels
			if x + 1 < width:
				gray_img[y, x + 1]     = min(255, max(0, gray_img[y, x + 1] + int(quant_error * kernel[0, 3])))
			if x + 2 < width:
				gray_img[y, x + 2]     = min(255, max(0, gray_img[y, x + 2] + int(quant_error * kernel[0, 4])))

			if y + 1 < height and x - 2 >= 0:
				gray_img[y + 1, x - 2] = min(255, max(0, gray_img[y + 1, x - 2] + int(quant_error * kernel[1, 0])))
			if y + 1 < height and x - 1 >= 0:
				gray_img[y + 1, x - 1] = min(255, max(0, gray_img[y + 1, x - 1] + int(quant_error * kernel[1, 1])))
			if y + 1 < height:
				gray_img[y + 1, x]     = min(255, max(0, gray_img[y + 1, x    ] + int(quant_error * kernel[1, 2])))
			if y + 1 < height and x + 1 < width:
				gray_img[y + 1, x + 1] = min(255, max(0, gray_img[y + 1, x + 1] + int(quant_error * kernel[1, 3])))
			if y + 1 < height and x + 2 < width:
				gray_img[y + 1, x + 2] = min(255, max(0, gray_img[y + 1, x + 2] + int(quant_error * kernel[1, 4])))

			if y + 2 < height and x - 2 >= 0:
				gray_img[y + 2, x - 2] = min(255, max(0, gray_img[y + 2, x - 2] + int(quant_error * kernel[2, 0])))
			if y + 2 < height and x - 1 >= 0:
				gray_img[y + 2, x - 1] = min(255, max(0, gray_img[y + 2, x - 1] + int(quant_error * kernel[2, 1])))
			if y + 2 < height:
				gray_img[y + 2, x]     = min(255, max(0, gray_img[y + 2, x    ] + int(quant_error * kernel[2, 2])))
			if y + 2 < height and x + 1 < width:
				gray_img[y + 2, x + 1] = min(255, max(0, gray_img[y + 2, x + 1] + int(quant_error * kernel[2, 3])))
			if y + 2 < height and x + 2 < width:
				gray_img[y + 2, x + 2] = min(255, max(0, gray_img[y + 2, x + 2] + int(quant_error * kernel[2, 4])))

	return np.clip(gray_img, 0, 255).astype(np.uint8)

Das Dithering von Computergrafiken ist heute nicht mehr notwendig. Das Aufkommen von Display-Technologien wie E-Paper könnte dieser Technik jedoch zu einer Renaissance verhelfen. E-Paper-Displays sind hochauflösende passive Displays, deren Pixel nicht selbst leuchten oder die von vorne beleuchtet werden. Die Pixel können nur wenige Helligkeitswerte abbilden. Ein perfekter Anwendungsfall für Dithering!

Monochromes Video eines Wasserfalls, das mittels Dithering erstellt wurde.

Quellenverzeichnis

Dieser Artikel basiert auf Informationen aus folgenden Quellen:

1. Tanner Helland: "Image Dithering: Eleven Algorithms and Source Code" online; TannerHelland.com; 2012-12-28
2. David Kadavy: "Why Monet Never Used Black, & Why You Shouldn’t Either" online; designforhackers.com; 2015-09-06
3. Steve Bagley: "Ordered Dithering - Computerphile" online; Video; Youtube/Computerphile