Die Mandelbrot-Menge

Beim zoomen in die Mandelbrotmenge offenbaren sich immer neue Kopien der Menge selbst. Diese Selbstähnlichkeit ist ein Merkmal von Fraktalen.

Benoît B. Mandelbrot - Vater der fraktalen Geometrie

Benoît B. Mandelbrot, der Vater der fraktalen Geometrie. (Portait mit KI-generiert; OpenAI/Dall-E)

Benoît B. Mandelbrot (20 November 1924 – 14 October 2010) war ein französisch-amerikanischer Mathematiker (Bild ?). Den größten Teil seines Berufslebens forschte er am Thomas J. Watson Research Center, dem Sitz der Forschungsabteilung von IBM. Auf ihn gehen der Begriff "Fraktal" und die Entdeckung der nach ihm benannten Mandelbrot-Menge zurück.

Diese Zahlenmenge, im deutschen Sprachgebrauch auch "Apfelmännchen" genannt, bildet eine fraktale geometrische Struktur. Sie entsteht durch Untersuchung der Glieder der komplexwertigen Reihe mit dem Startwert:

\[ z_0 = 0 \]

und der Bildungsformel:

\begin{equation} \label{eq:formel_mandelbrot} z_{n+1} = z_n^2 + c \end{equation}

Komplexe Zahlen sind eine Erweiterung der reellen Zahlen. Sie bestehen aus einem Realteil und einem Imaginärteil und werden in der Form z = a + bi dargestellt, wobei i die sogenannte imaginäre Einheit ist. Eine komplexe Zahl steht also für einen Punkt in der komplexen Zahlenebene, die durch die Realachse und die Imaginärachse gebildet wird. Bildlich gesprochen steht eine komplexe Zahl für einen Vektor, der vom Ursprung (0,0) zu dem Punkt (a,b) in der komplexen Zahlenebene zeigt. Der Realteil a ist die Projektion des Vektors auf die Realachse und der Imaginärteil b ist die Projektion auf die Imaginärachse.

Die Zahlen der komplexen Ebene, für welche diese Reihe nicht gegen unendlich geht, gehören zur Mandelbrot-Menge. Alle anderen Zahlen gehören nicht dazu. Das erstaunliche dieser Menge ist, dass obwohl die Bildungsformel sehr einfach ist, die Grenzlinie zwischen der Mandelbrot-Menge und dem Rest der komplexen Zahlen eine sehr komplizierte Struktur bildet. Die Menge wurde daher auch als eines der kompliziertesten Objekte in der Mathematik beschrieben [1a]. Benoît Mandelbrot selbst nannte solche Gebilde Fraktale.

Das herausragende Merkmal fraktaler Strukturen ist ihre Selbstähnlichkeit. Egal auf welcher Größenskala man sie betrachtet, man findet immer wieder ähnliche Formen. Sie beruhen oft auf sehr einfachen Regeln, die aber zu einer unglaublichen Formenvielfalt führen. Diese Selbstähnlichkeit ist eine Eigenschaft, die auch in der Natur seit Anbeginn des Lebens zu finden ist, und das Studium der Fraktale hat dazu beigetragen, die Entstehungs- und Wachstumsprozesse in der Natur besser zu verstehen. Die Mandelbrot-Menge ist ein Beispiel für diese Eigenschaft und war der Auslöser für die Popularisierung der fraktalen Geometrie in den 1980iger Jahren des 20. Jahrhunderts.

Die in diesem Artikel verwendeten Bilder wurden mit dem Python-Skript mandelbrot_interactive.py aus dem Archiv "Unterhaltungsmathematik mit Python" erstellt. Es rechnet parallel auf mehreren Prozessoren und verfügt über eine Vielzahl an Optionen, welche das Rendern verschiedener Orbit-Traps ermöglichen.

Lage der in der komplexen Zahlenebene

Eine komplexe Zahlenreihe, welche durch die oben angegebene Formel gebildet wird, nennt man auch Orbit. Berechnet man die Länge der Orbits für alle Punkte der komplexen Zahlenebene im Bereich von -2 bis 2 auf der Realachse und -1.5 bis 1.5 auf der Imaginärachse, so erhält man das folgende Bild. Durch Bewegen des Mauszeigers über das Bild werden in gelber Farbe die Orbits des zur Mausposition gehörenden Startpunktes dargestellt.

Mandelbrot-Live-Applet mit Orbitvorschau

Dieses Javascript-Applet berechnet die Mandelbrot Menge in der komplexen Zahlenebene. Ausgehend von der aktuellen Position d es Mauszeigers wird der Orbit der dazugehörigen Zahlenreihe in gelber Farbe dargestellt. Linke Maustaste: Spur behalten; Rechte Maustaste: Spuren löschen.

Unendliche Formenvielfalt beim Zoom in die Tiefe

Je näher man dem Rand der Mandelbrot-Menge kommt, desto mehr Iterationen sind notwendig, um festzustellen, ob ein Punkt divergiert oder nicht. Es ist jedoch mathematisch bewiesen, dass die Folge divergent sein muss, wenn eine Zahl der Bahn den Absolutbetrag 2 überschreitet. Mit diesem Wissen kann viel Zeit bei Berechnungen außerhalb der Menge gespart werden.

Punkte, die nicht divergieren, sind Teil der Mandelbrotmenge und werden schwarz dargestellt. Um den Grenzbereich visuell aufzulösen werden sehr viele Iterationen benötigt. Die Entscheidung ob ein Punkt Teil der Menge ist dauer immer länger, je tiefer man in die Menge hineinzoomt. Während man ein Übersichtsbild mit 250 Iterationen berechnen kann, muß man bei hochauflösenden Detailaufnahmen mit tausenden von Iterationen rechnen.

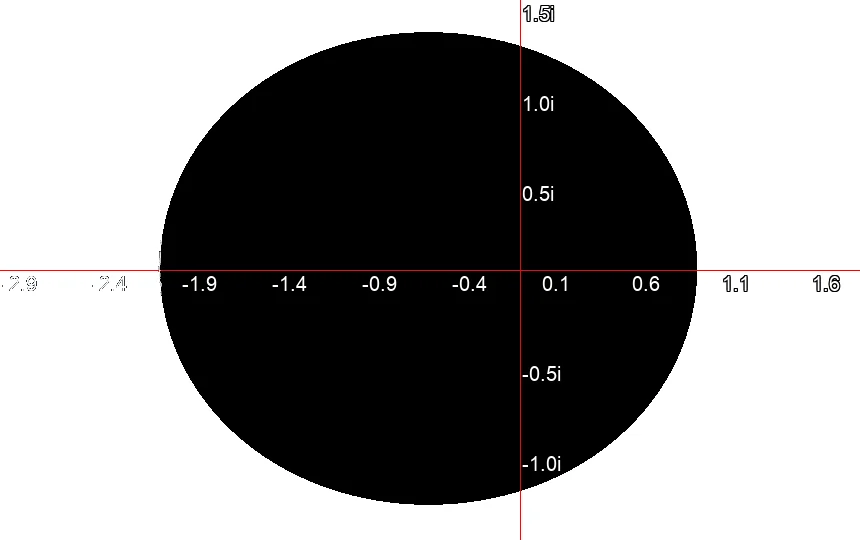Mandelbrot-Menge nach einer Iteration.
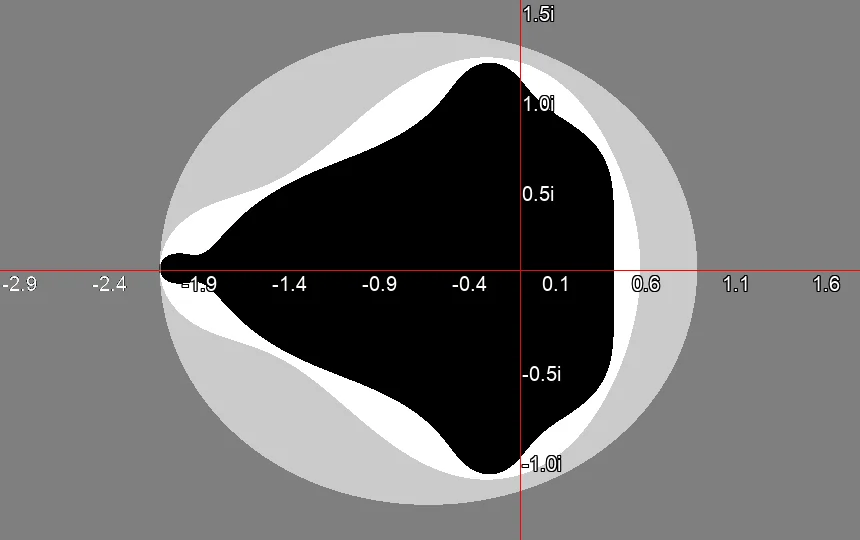Mandelbrot-Menge nach drei Iteration.
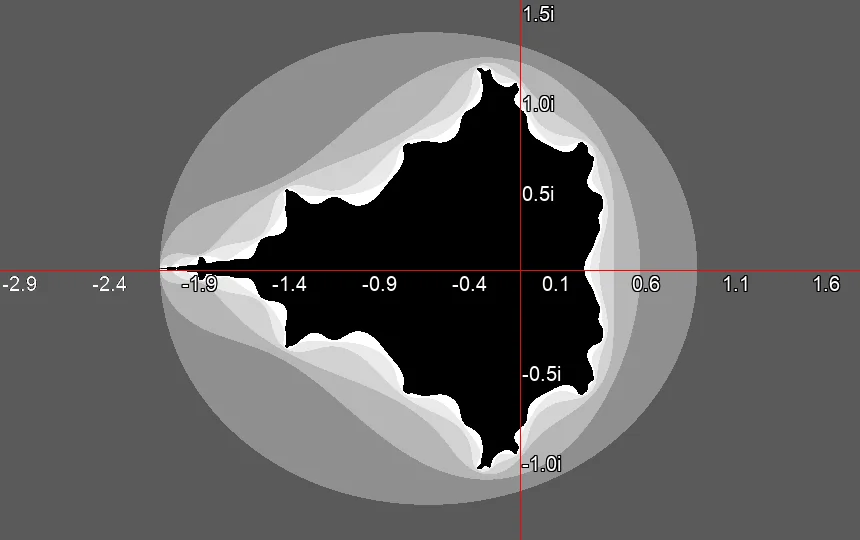Mandelbrot-Menge nach sieben Iteration.
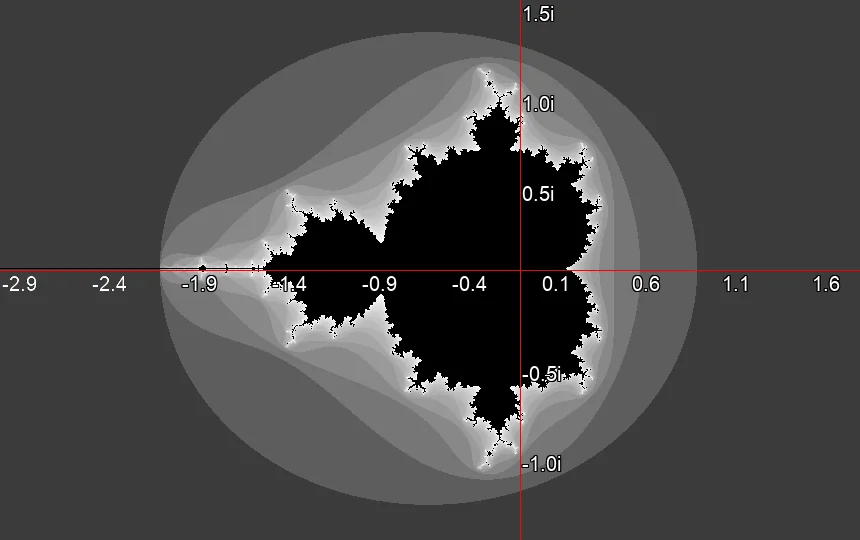Mandelbrot-Menge nach 19 Iteration.

Die Mandelbrot-Menge ist zusammenhängend [4]. Der Bereich in dem die Zahlenfolge konvergiert, also das Innere der Menge, bildet keine Inseln. Alles darin ist durch dünne Filamente verbunden. Der Grenzbereich ist sehr komplex und enthält viele interessante Strukturen (Bild ?), die erst beim Heranzoomen sichtbar werden.

Der Rand der Mandelbrot-Menge ist voller komplexer Strukturen.
Beim hineinzoomen zeigen sich immer neue, feine Strukturen und Spiralen.
Immer wieder tauchen auch verkleinerte Kopien der Mandelbrot-Menge auf.

Man findet Wirbel, Spiralen (Bild ?) und immer wieder verkleinerte Kopien der Menge selbst (Bild ?). Es ist eine Welt voller wunderbarer Details, die sich endlos in immer neuen Variationen wiederholen, nur begrenzt durch die Rechenleistung des Computers. Denn letztendlich wären unendlich viele Iterationen nötig, um die Mandelbrotmenge vollständig zu berechnen.

Die Kunst der Farbgebung

Die Farbwahl hat einen entscheidenden Einfluß auf die Darstellung der Mandelbrot-Menge. Seit ihrer Entdeckung wurden eine Vielzahl von, immer künstlerischer anmutenden Farbschemata entwickelt.

Iterationsbasierte Farbschemen

Die ersten Darstellungen der Mandelbrot-Menge waren schwarz-weiß und zeigten, wie in Bild ? nur die zur Menge selbst gehörenden Punkte in schwarzer Farbe. Dies war ursprünglich den begrenzten Möglichkeiten der damaligen Computer geschuldet, da die Ausgabe häufig noch auf Papier oder monochromen Monitoren erfolgte. Auch heute zeigen die meisten Darstellungen des Mandelbrot-Fraktals die Menge selbst nur als schwarze Fläche. Eingefärbt werden meist nur die Pixel, die nicht zur Menge gehören, deren zugehörige Orbits also divergent sind.

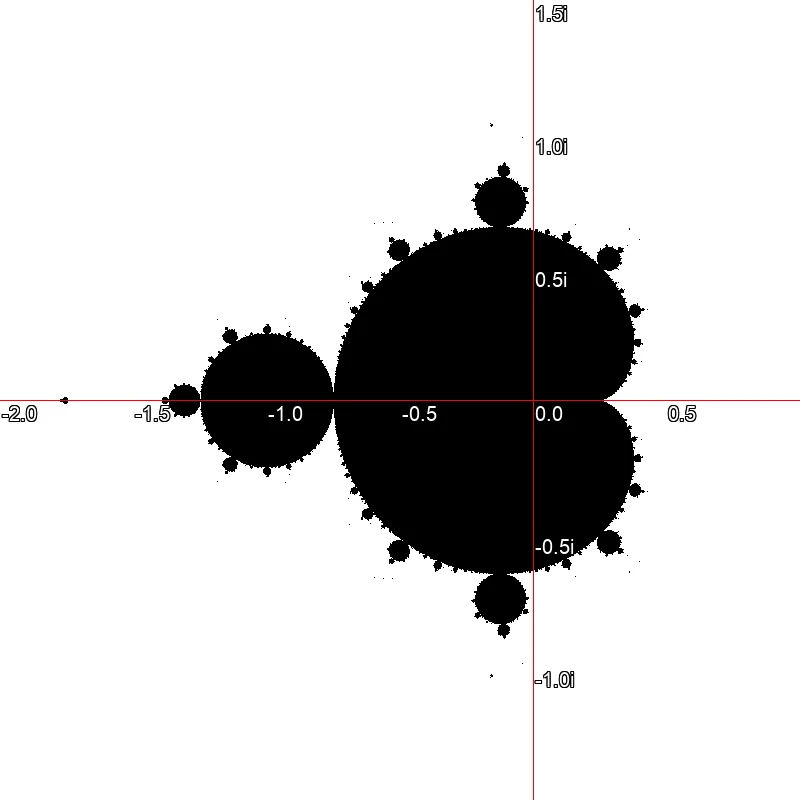Schwarzweißdarstellung der Mandelbrotmenge. Die schwarzen Pixel gehören zur Menge, die weißen gehören nicht dazu.
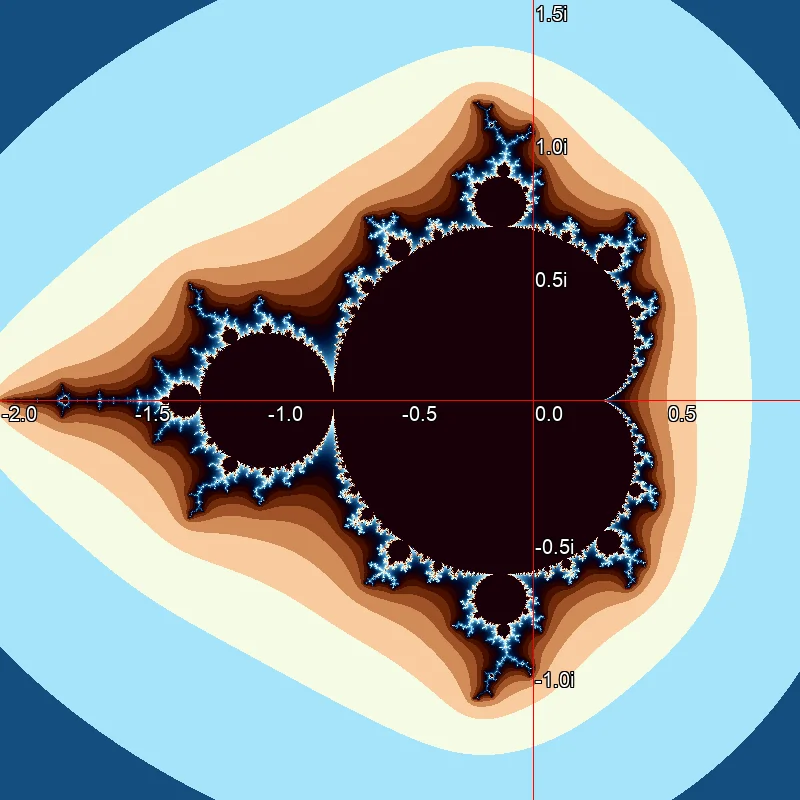Bei Farbgebung gemäß dem Logarithmus des Iterationszählers zeigen sich Bänderartige übergänge. Das liegt daran, daß die Anzahl der Iterationen eine Ganzzahl ist.
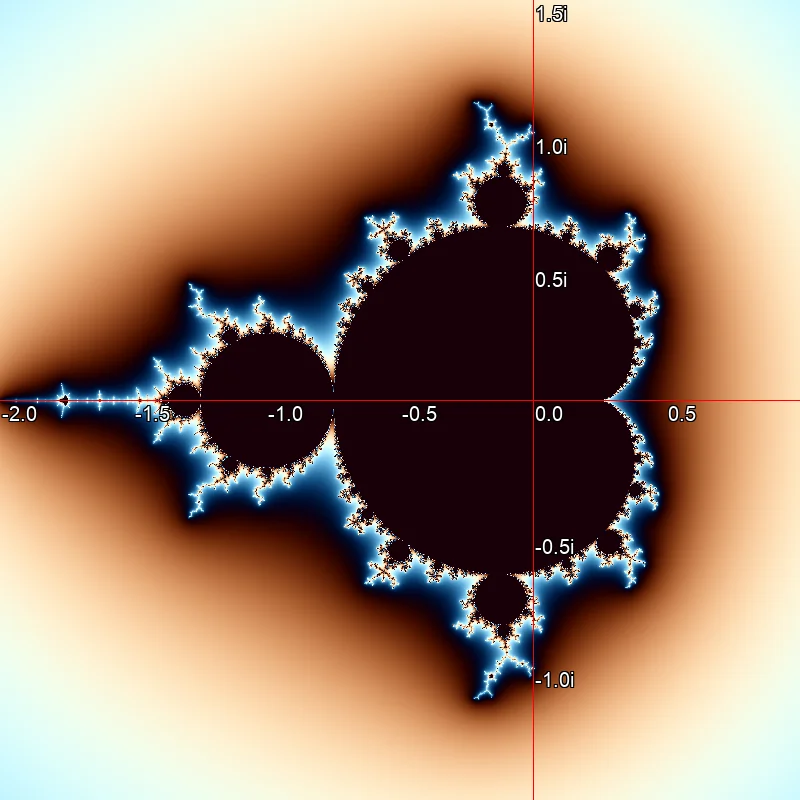Kontinuierliche Farbgebung nach dem, von Linas Vepstas beschriebenen Algorithmus.[2].

Mit dem Aufkommen von Heimcomputern in den 1980er Jahren war es dann lange Zeit üblich, die Anzahl der durchgeführten Iterationen zu zählen und diesen Wert mit Hilfe von Farbtabellen in eine Farbe umzuwandeln. Später, als sich die Computergrafik verbesserte, wurde der Logarithmus des Iterationszählers berechnet und mit Hilfe von Formeln, wie in Bild ? dargestellt in einen R,G,B-Wert umgewandelt. In den 1990iger Jahren wurde schließlich eine Methode populär, welche es ermöglichte, die Farben der Mandelbrot-Menge, wie in Bild ? dargestellt, kontinuierlich zu berechnen [2]. Diese Methode liefert die schönsten Ergebnisse und wurde in den oben gezeigten Bildern verwendet. Der sogenannte Smooth-Iteration-Count berechnet sich nach folgender Formel:

\begin{equation} v = n + 1 - \frac{\log(\log(|z_n|))}{\log(2)} \end{equation}

wobei:

  • \(v\) Der kontinuierliche Iterationszähler. Der Wert für die Farbgebung des Pixels.
  • \(n\) Anzahl der Iterationen bis zum Abbruch
  • \(z_n\) Kompler Wert der Zahlenreihe nach n Iterationen.

Orbit Traps

Geometrische Orbit-Traps

Beim Berechnen der Mandelbrot-Menge wird für jeden Punkt der komplexen Ebene eine Zahlenfolge, der sogenannte Orbit berechnet. Eine weitere Möglichkeit die Fraktale interessanter zu gestalten, sind sogenannte Orbit-Traps. Dies sind im einfachsten Fall geometrische Formen, die auf der komplexen Ebene verteilt werden. Für jeden Punkt eines Orbits wird der Abstand zu diesen Formen berechnet. Dieser Wert wird dann als Kriterium für die Einfärbung oder auch für einen vorzeitigen Abbruch der Iteration verwendet. Da diese Strukturen bei Kontakt die Iteration beenden, werden sie Orbitfallen (engl.: Orbit-Traps) genannt. Als einfache Orbit-Traps können z.B. die Real- und Imaginärachsen selbst, der Koordinatenursprung, ein Einheitskreis oder auch beliebig positionierte Punkte dienen.

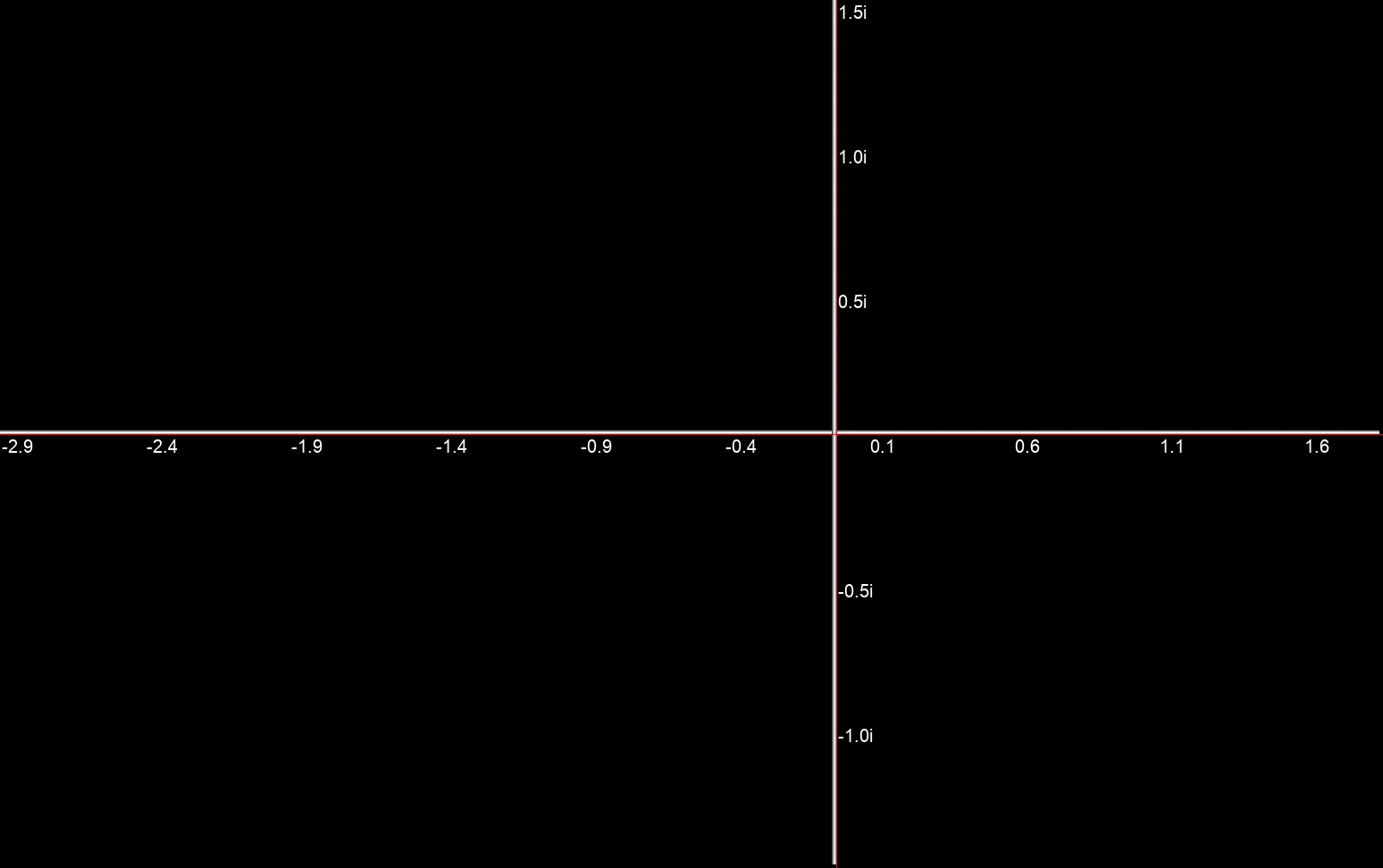Real und Imaginärachse als geometrische Orbit-Trap.
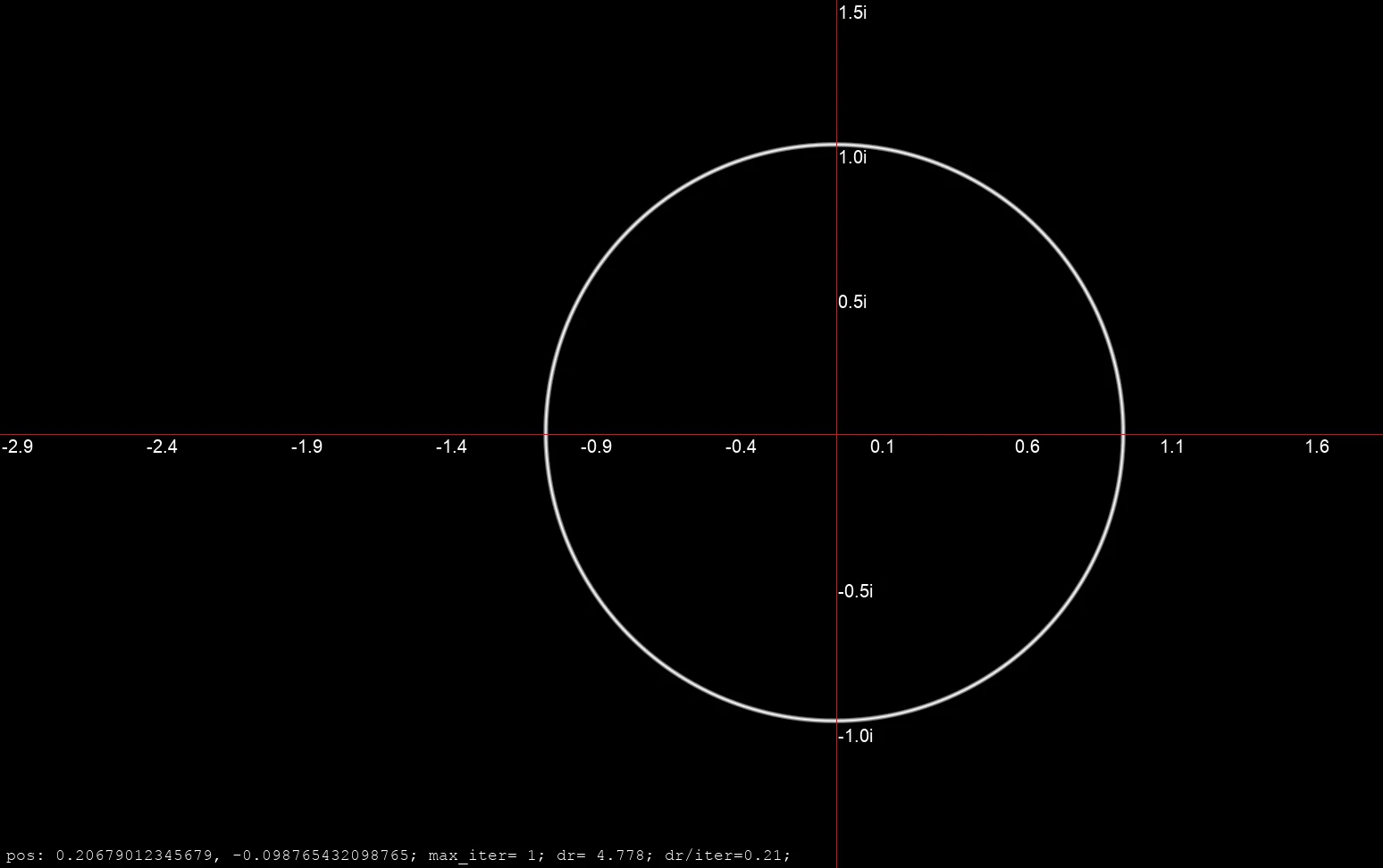Einheitskreis als geometrische Orbitfalle.
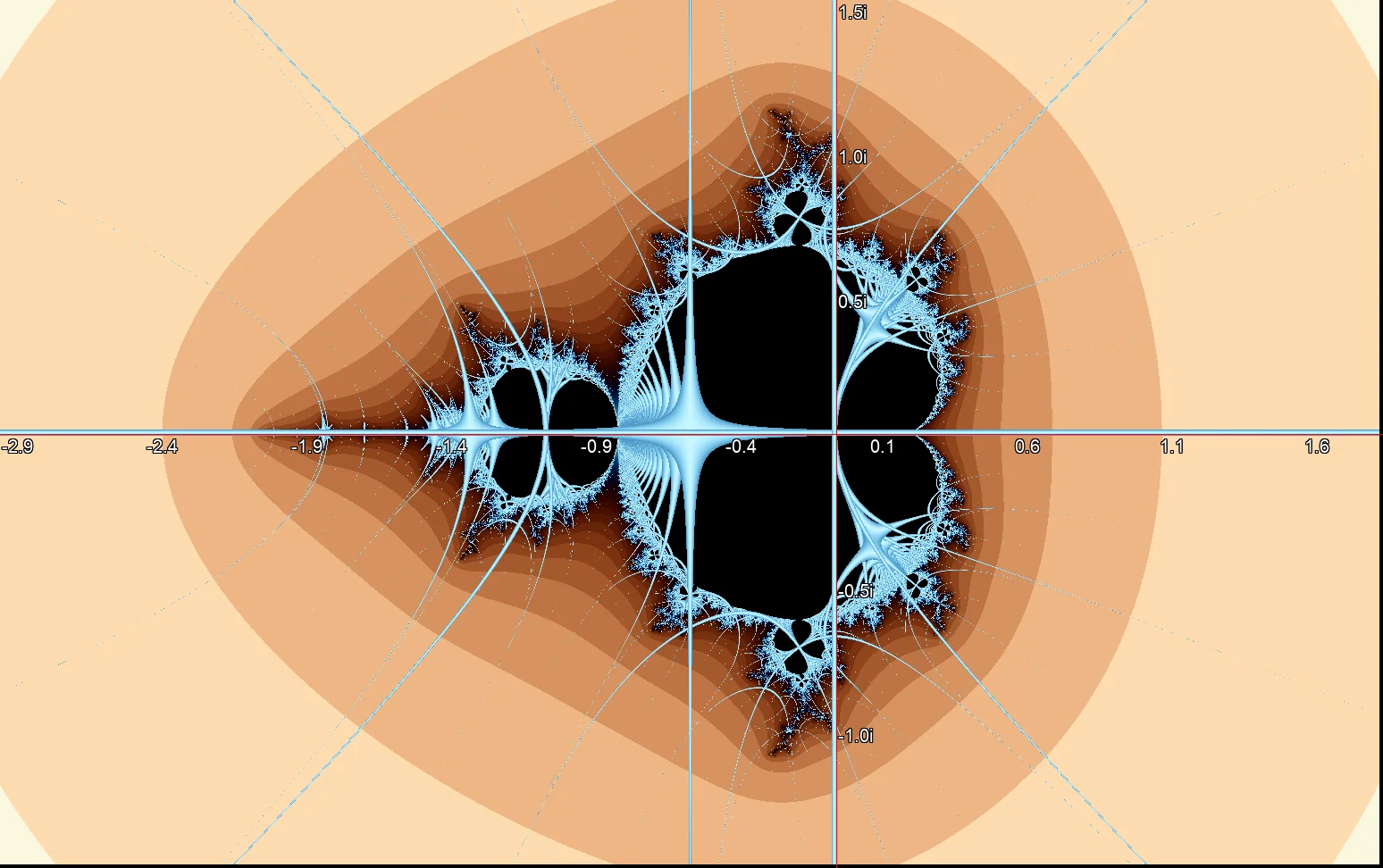Mandelbrot Rendering mit Real und Imaginärachse als geometrische Orbit-Trap.
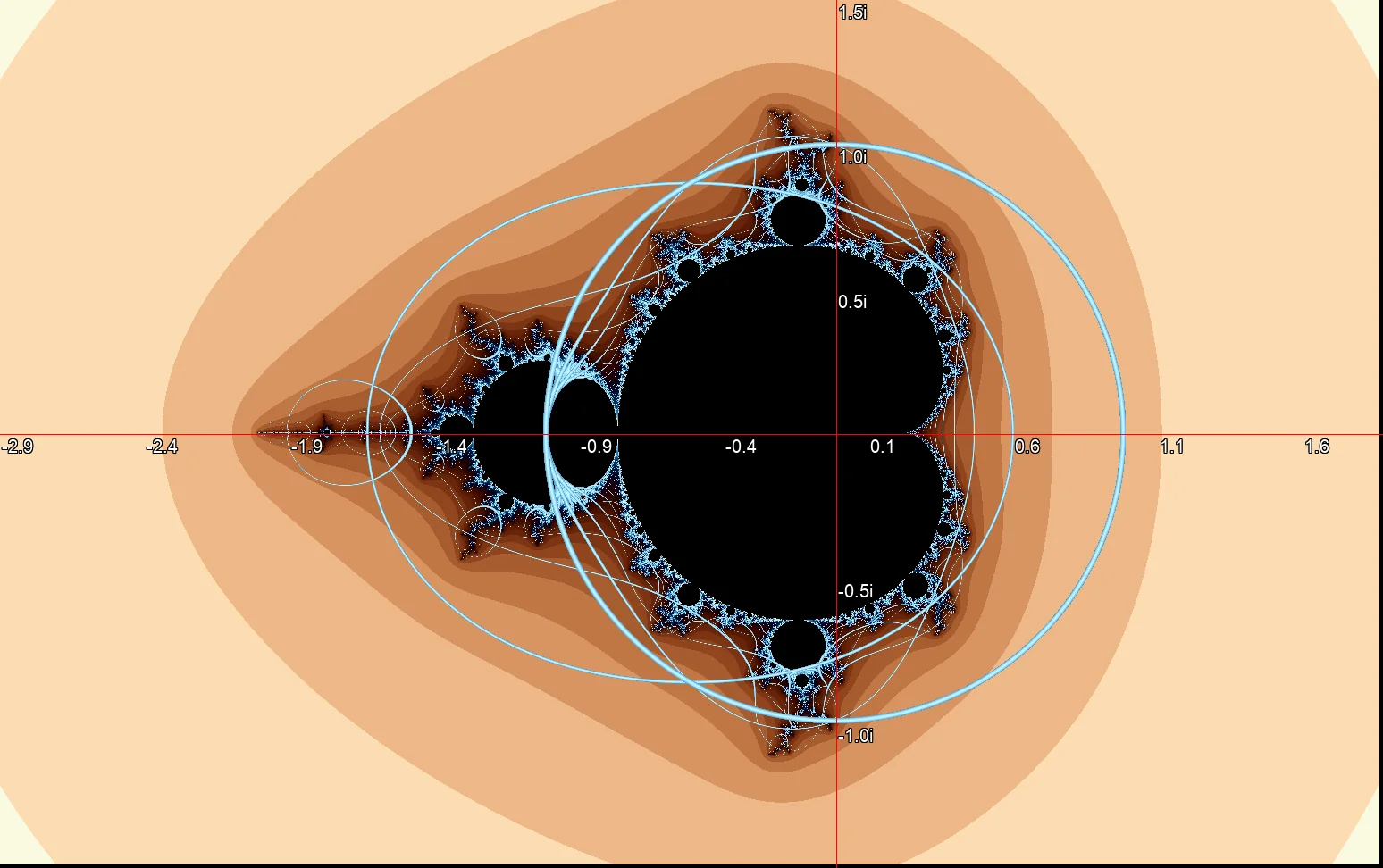Mandelbrot Rendering mit dem Einheitskreis als geometrische Orbitfalle.

Das folgende Quellcodebeispiel zeigt die Hauptschleife der Implementierung einer geometrischen Orbit-Trap in Python. Die Falle ist eine Kombination aus einem Kreis und den Achsen der komplexen Zahlenebene. Das Ergebnis ist in Bild ? dargestellt. Es wird nur das Resultat bei Iterationsabbruch durch den Kontakt mit der Orbitfalle gezeichnet. Die Umrisse der Mandelbrotmenge sind nur noch im Hintergrund sichtbar.

Rendering einer geometrischen Orbitfalle, gebildet von den Achsen der komplexen Ebene und einem Kreis mit Radius 0.27 um den Koordinatenursprung. 
def compute_mandelbrot(dimx : int, dimy : int, 
	maxiter : int, rmin : float, rmax : float, imin : float, imax : float):
    istep = (imax - imin) / dimy
    rstep = (rmax - rmin) / dimx
    mandelbrot_set = np.zeros((dimy, dimx), dtype=np.float64)

    for row in range(dimy):
        for col in range(dimx):
            z = 0
            c = (rmin + col * rstep) + 1j * (imin + row * istep)

            trapped = False
            trap_size = 0.025
            trap_dist = 0
            trap_radius = 0.27
            for k in range(maxiter):
                z = z*z + c

                # circular orbit trap
                if (trap_radius-trap_size) < abs(z) < (trap_radius + trap_size):
                    trap_dist = abs(trap_radius - abs(z))
                    trapped = True

                # real axis trap
                if abs(z.real) < trap_size:
                    trap_dist = abs(z.real)
                    trapped = True
                
                # imaginary axis trap
                if abs(z.imag) < trap_size:
                    trap_dist = abs(z.imag)
                    trapped = True

                if abs(z) > 2 or trapped:
                    break

            mandelbrot_set[row, col] = 0 if not trapped else trap_dist

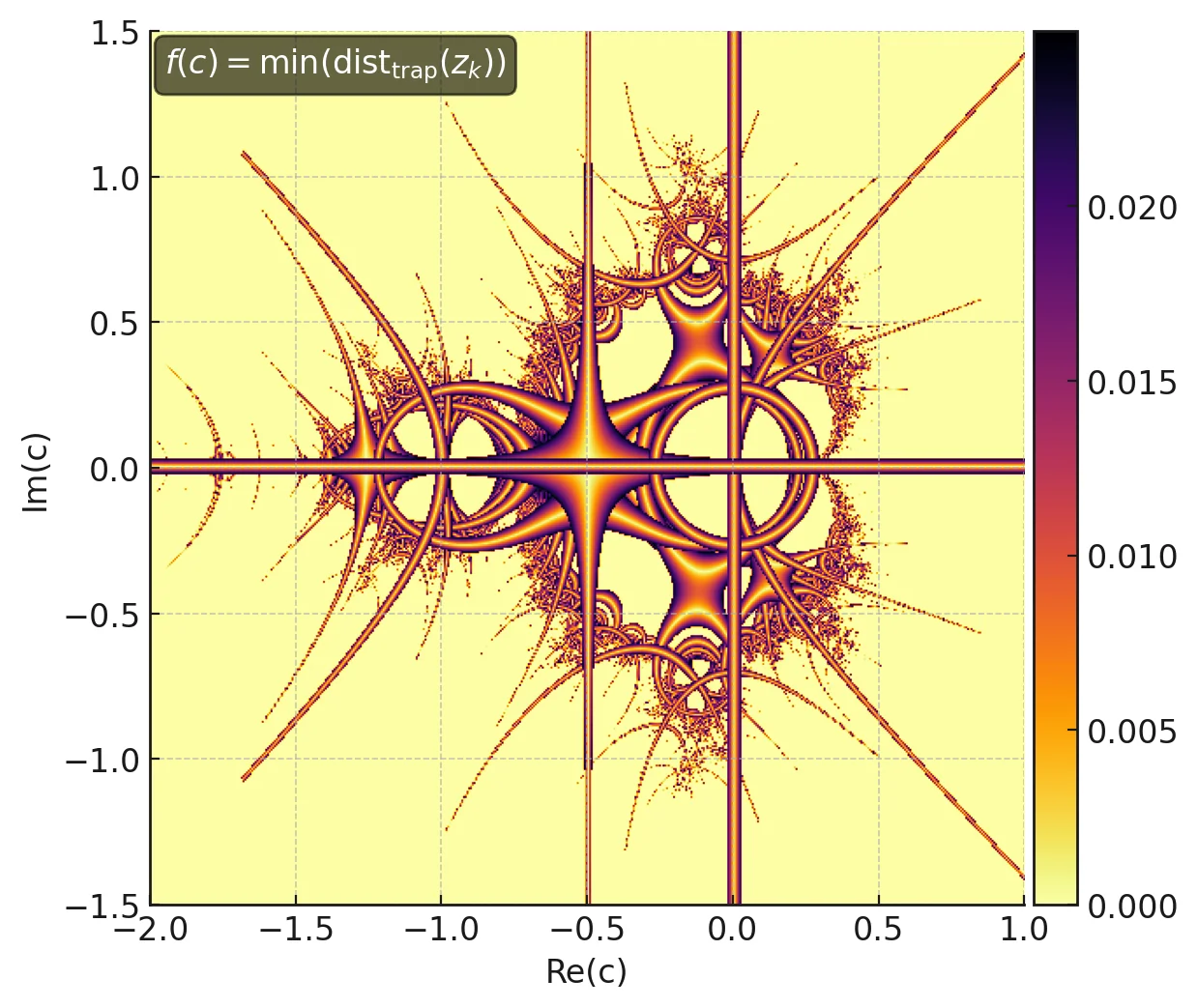
    return mandelbrot_set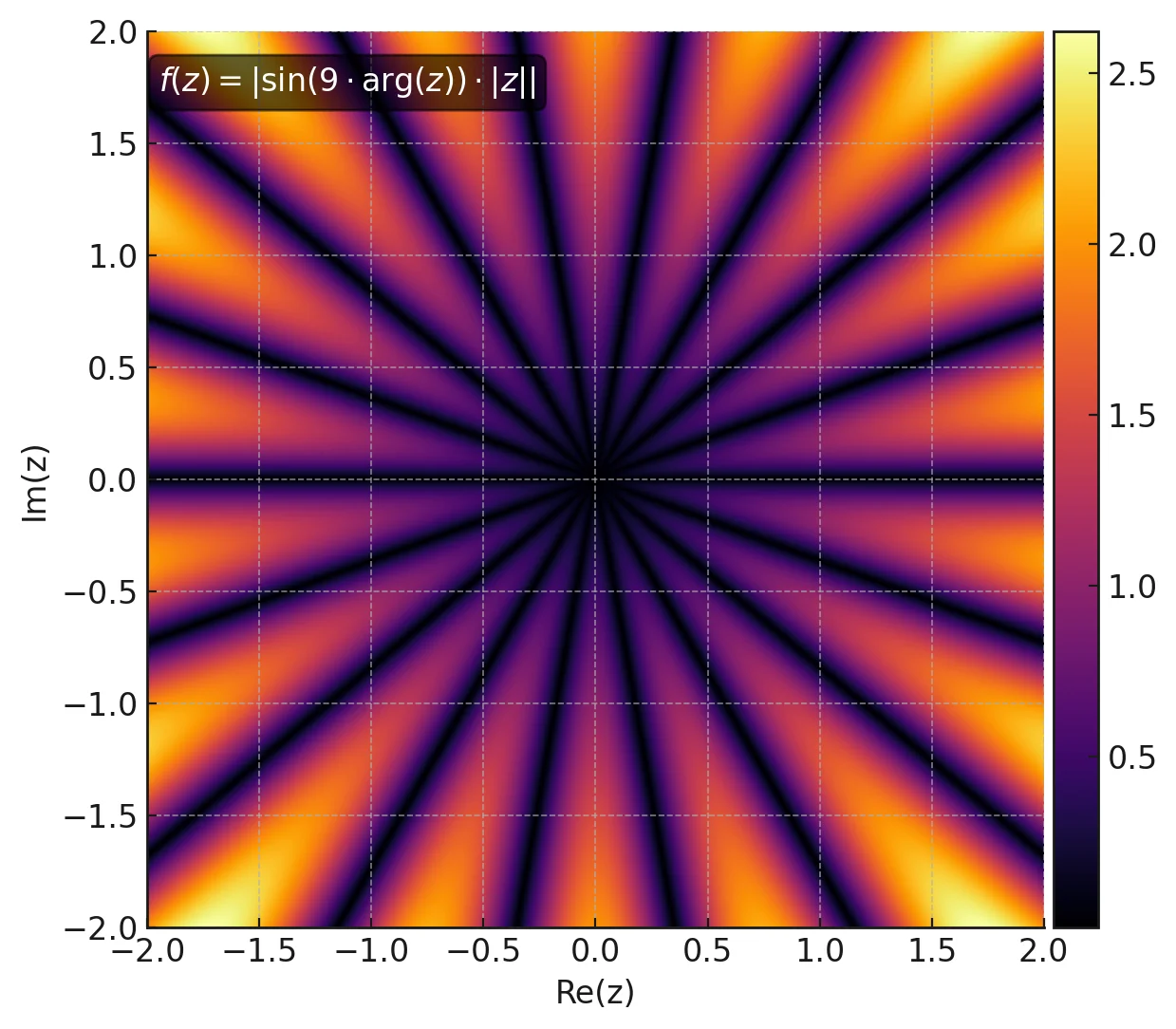

Funktionen als Orbit-Traps

Blütenförmige Orbit-Trap-Funktion mit 18-facher Winkelsymmetrie Das Bild zeigt eine blütenförmige Orbit-Trap-Funktion mit 18-facher Winkelsymmetrie.

Man kann auch zweidimensionale Funktionen \( f : \mathbb{C} \to \mathbb{R} \) oder sogar Bilder als Orbitfallen verwenden. Dabei nimmt man den Minimalwert \(d_{\text{trap}}\) der Funktion \( f(z_n) \) entlang aller Punkte des Orbits als Kriterium für die Farbgebung. Alternativ könnte man die Fallenentfernung \(d_{\text{trap}}\) auch als zusätzliches Iterationsabbruchkriterium verwenden. Für die folgenden Mandelbrot-Bilder wird die in Bild ? dargestellte Orbit-Trap-Funktion verwendet:

\begin{equation} \label{eq:trap_function} f : \mathbb{C} \to \mathbb{R}, \quad f(z) = \left| \sin\left(9 \cdot \arg(z)\right) \cdot |z| \right| \end{equation}

Die "Fallenentfernung" eines Orbits ergibt sich dann aus:

\begin{equation} \label{eq:trap_color} d_{\text{trap}} = \min_n f(z_n) = \min_n \left| \sin\left(9 \cdot \arg(z_n)\right) \cdot |z_n| \right| \end{equation}

Nun kann man noch wählen, ob die Falle nur im Kernbereich des Fraktals, also den Elementen der Menge selbst (Bild ?), oder in der gesamten komplexen Zahlenebene (Bild ?) wirken soll. Geometrische Orbitfallen erzeugen oft organisch anmutende Strukturen. Beim Hineinzoomen in das Fraktal entstehen dann dreidimensional wirkende Muster.

Mandelbrot mit rosettenförmiger Orbit-Trap. Die Falle beeinflußt nur die Farbgebung der Elemente Mandelbrot Menge selbst. Anstelle die Punkte schwarz zu färben, wird die Entfernung zur Falle als Farbgebungskriterium verwendet. Der Randbereich wird, wie gehabt mittels Smooth-Iteration-Count eingefärbt.
Hier wird die gleiche rosettenförmige Orbit-Trap verwendet. Anstelle der Iterationsanzahl wird jedoch für alle Punkte der komplexen Zahlenebene die Entfernung zur Falle als Kriterium für die Farbgebung verwendet. Die Iterationen werden wie gehabt durchgeführt aber die Anzahl der Iterationen wird nicht mehr für die Farbgebung verwendet.

Quellcodebeispiel mit kontinuierlicher Farbgebung und Orbit-Trapfunktion

Abschließend folgt ein einfaches Beispiel zur Berechnung einer Mandelbrot-Menge mit Orbitfalle und kontinuierlicher Farbgebung. Die Implementierung erfolgt in Python unter Verwendung der Pygame-Bibliothek sowie Numba, einem "Just-in-Time"-Compiler. Das Beispiel ist so gehalten, dass es sich leicht an eigene Bedürfnisse anpassen lässt.

Mandelbrot-Menge mit rosettenförmiger Orbitfalle und kontinuierlichem Iterationszähler.

Das Code-Beispiel verwendet die in Bild ? gezeigte Funktion \[ f : \mathbb{C} \to \mathbb{R}, \quad f(z) = \left| \sin\left(9 \cdot \arg(z)\right) \cdot |z| \right| \] als Orbitfalle. Das Ergebnis der Berechnung des minimalen Wertes dieser Funktion für die komplexen Werte \( z_n \) eines Orbits bestimmt die Farbgebung der Elemente in der Mandelbrotmenge. Zusätzlich wird dieser Wert, leicht herunterskaliert, zum Wert des kontinuierlichen Iterationszählers im Außenbereich addiert. Dadurch zeigen sich die Strukturen der Orbitfalle auch im Außenbereich des Fraktals. 

import pygame
import numpy as np
from numba import jit


@jit
def trap_function(z, petals=5):
    return abs(np.sin(petals * np.angle(z)) * np.abs(z))


@jit
def compute_mandelbrot(dimx : int, dimy : int, maxiter : int, rmin : float, rmax : float, imin : float, imax : float):
    istep = (imax - imin) / dimy
    rstep = (rmax - rmin) / dimx
    mandelbrot_set = np.zeros((dimy, dimx), dtype=np.float64)

    escape_radius = 100
    petals = 9
    for row in range(dimy):
        for col in range(dimx):
            z = 0
            c = (rmin + col * rstep) + 1j * (imin + row * istep)

            dist = 1e10
            for k in range(maxiter):
                z = z*z + c

                # compute minimum distance to trap function
                dist = min(dist, trap_function(z, petals))

                if abs(z) > escape_radius:
                    # if a point is in the Mandelbrot-Set
                    mandelbrot_set[row, col] = k + 1 - np.log(np.log(np.abs(z))) / np.log(2)
                    mandelbrot_set[row, col] += 0.5*dist
                    break

            else:
                # if a point is outside of the Mandelbrot-Set
                mandelbrot_set[row, col] = dist * 40

    return mandelbrot_set


def main(width, height, max_iter):
    pygame.init()
    pygame.display.set_caption("Mandelbrot-Set")
    screen = pygame.display.set_mode((width, height))

    imin, imax = -1.5, 1.5
    rmin, rmax = -(0.5*(imax-imin)) * (width/height)-.5, (0.5*(imax-imin)) * (width/height)-.5

    mandelbrot_array = compute_mandelbrot(width, height, max_iter, rmin, rmax, imin, imax)
    mandelbrot_array = np.log(mandelbrot_array + 1)
    mandelbrot_array /= np.max(mandelbrot_array)

    mask = mandelbrot_array != 0
    start, freq = 1, 9
    r = mask * (0.5 + 0.5*np.cos(start + mandelbrot_array * freq + 0))
    g = mask * (0.5 + 0.5*np.cos(start + mandelbrot_array * freq + 0.6))
    b = mask * (0.5 + 0.5*np.cos(start + mandelbrot_array * freq + 1.0))

    r = (r / np.max(r) * 255).astype(np.uint8)
    g = (g / np.max(g) * 255).astype(np.uint8)
    b = (b / np.max(b) * 255).astype(np.uint8)

    surface = pygame.surfarray.make_surface(np.stack([r.T, g.T, b.T], axis=-1))
    screen.blit(surface, (0, 0)) 
    pygame.display.update()
    pygame.image.save(screen, f"mandelbrot.png")

    while not any(event.type == pygame.QUIT for event in pygame.event.get()):
        pass

    pygame.quit()


if __name__=="__main__":
    main(1920, 1080, 500)

Quellenverzeichnis

  1. "Computer-Kurzweil" Spektrum der Wissenschaft: Verständliche Forschung, 1992, ISBN 3-922508-50-2; a: Seite 13
  2. Linas Vepstas: "Renormalizing the Mandelbrot Escape" online
  3. Rico Mariani: "The Mariani-Silver Algorithm for Drawing the Mandelbrot Set" online;
  4. Adrien Douady, John H. Hubbard: Exploring the Mandelbrot set. The Orsay Notes. online; Based on course notes: A. Douady “Holomorphic dynamical Systems” 1983-1984