Das Chaosspiel

Verschiedene vom Chaosspiel erzeugte Fraktale

Die ersten 7 Schritte des Chaosspiels für die Eckpunkt Reihenfolge ACABBCB.

Das fertige Sierpinski-Dreieck

Was ist das Chaosspiel?

Als Fraktal bezeichnet man in der Mathematik selbstähnliche Muster. Das sogenannte Chaosspiel (auch Zufalls-Iterations-Algorithmus genannt) ist eine Methode, um Iterativ Fraktale mit der Hilfe von Polygonen bzw. beliebigen zweidimensionalen Punktverteilungen zu erzeugen. [3]

Die Regeln sind einfach und sollen am Beispiel eines Dreiecks erklärt werden. Dieses hat die Eckpunkte A, B und C. Man startet das Chaosspiel an einem zufälligen Punkt P1 innerhalb des Dreiecks. Um die nächste Position P2 zu berechnen, wählt man zufällig einen der drei Eckpunkte des Dreiecks und setzt P2 in die Mitte der Strecke zwischen dem Punkt P1 und dem zufällig gewählten Eckpunkt. Diesen Vorgang wiederholt man beliebig oft und zeichnet jeden erhaltenen Punkt auf den Bildschirm.

Es fällt auf, dass einige Bereiche des Dreiecks in späteren Schritten nicht mehr erreicht werden können. Es entsteht ein fraktales Muster. Lediglich die ersten Schritte (im Bild Orange) können in diesen Teilbereichen landen, alle weiteren Punkte (im Bild Grün) landen dazwischen. Das so entstehende Fraktal heißt Sierpinski-Dreieck. Es wurde erstmals von dem polnischen Mathematiker Wacław Sierpiński im Jahr 1915 beschrieben. Es taucht aber bereits in Fußbodenmustern im mittelalterlichen Rom auf [2].

Verallgemeinerung auf Beliebige Polygone

Dieser Konstruktionsmechanismus für Fraktale lässt sich auf beliebige Polygone bzw. zweidimensionale Punktverteilungen anwenden. Allerdings sollte man, wenn man die Anzahl der Ecken erhöht die Strecke nicht mehr halbieren, sondern den Faktor leicht anpassen, andernfalls ergibt sich nicht immer ein Fraktal. Halbiert man die Strecke zwischen der aktuellen Position und der zufällig ausgewählten Ecke bei einem Viereck, so erhält man beispielsweise eine gleichmäßig gefüllte Fläche, kein Fraktal.

Die Halbierung der Strecke bei einem Dreieck entspricht der Multiplikation ihrer Länge mit dem Faktor 0.5. Verallgemeinert man das auf Polygone mit n-Ecken, so ergibt sich nach [1] ein günstiger Faktor für beliebige Polygone mit n Ecken näherungsweise aus der empirischen Gleichung:

Für diesen Faktor ergeben sich fraktale Muster, deren Selbstähnlichkeit sofort zu erkennen ist (z. B.: Dreiecke in Dreiecken in Dreicken). Die Ergebnisse von Durchläufen des Chaosspiels für Polygone mit 3, 4 und 5 Ecken sind in den folgenden Bildern dargestellt. Prinzipiell kann der Faktor r aber frei gewählt werden. Die besten Resultate erzielt man in der Regel mit Werten um 0.5.

n=3, r=0.5, zufällige Punktauswahl

n=4, r=0.5714, zufällige Punktauswahl

n=5, r=0.62, zufällige Punktauswahl

Für die Grafiken wurde zusätzlich jedem Eckpunkt eine andere Farbe zugewiesen. Die Farbe ergibt sich aus der Position des Eckpunktes im Farbkreis. Während der Berechnung wurde jeder neue Punkt mit der Farbe des Eckpunktes eingefärbt, in dessen Richtung er zuletzt gesprungen ist.

Einschränkungen in der Eckpunktauswahl

Bislang sehen die Fraktale trotz allem sehr regelmäßig aus. Um das zu ändern wird eine weitere Modifikation eingeführt. Die Eckpunkte werden nach wie vor zufällig ausgewählt, aber es werden Einschränkungen bei der Auswahl eingeführt. Solche Einschränkungen können beispielsweise sein:

• Ein Eckpunkt darf nicht zweimal hintereinander ausgewählt werden
• Wenn ein Eckpunkt ausgewählt wurde, so darf im nächsten Schritt keiner seiner Nachbarn ausgewählt werden.
• Wenn zweimal der gleiche Eckpunkt hintereinander ausgewählt wurde, muss im nächsten Schritt ein Eckpunkt gewählt werden, der mindestens 2 Ecken entfernt ist.

Der Phantasie sind hier keine Grenzen gesetzt. Insgesamt können in unserer Version des Zufalls-Iterations-Algorithmus jetzt folgende Dinge geändert werden:

• Die Anzahl der Eckpunkte des Basispolygones
• Der Faktor r, der festlegt, wie weit ein Punkt in einem Iterationsschritt in Richtung des zufällig gewählten Eckpunktes springt
• Zusätzliche Regeln, welche die "Zufälligkeit" der Eckpunktauswahl leicht einschränken

Die Ergebnisse von Durchläufen des Chaosspiels mit eingeschränkter Wahl der Eckpunkte sind im folgenden dargestellt.

n=5, r=0.5, zufällige Punktauswahl

n=5, r=0.5, Eckpunkte können nicht zweimal hintereinander gewählt werden.

n=5, r=0.5, Wenn ein Eckpunkt zweimal nacheinander gewählt wird, darf die nächste Wahl kein benachbarter Eckpunkt sein.

Alternative Methode der Farbgebung

Eine alternative Methode der Farbgebung besteht darin, das Chaosspiel mit leicht veränderten Parametern für jeden Farbkanal (Rot, Grün und Blau) getrennt laufen zu lassen. Bei diesem Ansatz ist den Eckpunkten des Polygones keine Farbe zugewiesen. Pixel auf dem Bildschirm werden in ihrer Helligkeit erhöht, wenn das Chaosspiel auf einem Pixel landet. Es wird nur die Helligkeit des Farbkanals erhöht, der dem jeweiligen Chaosspiel zugewiesen ist.

Das alleine würde nicht reichen, denn drei identische Chaosspiele auf drei Farbkanälen würden lediglich ein Graustufenbild erzeugen. Um mehr Farbe in die Simulation zu bringen, müssen sich die Parameter der drei Chaosspiele leicht unterscheiden. Das kann erreicht werden, indem der Parameter r für jedes der Chaosspiel minimal und zufällig modifiziert wird. Die folgenden drei Bilder zeigen das Ergebnis einer solchen Modifikation.

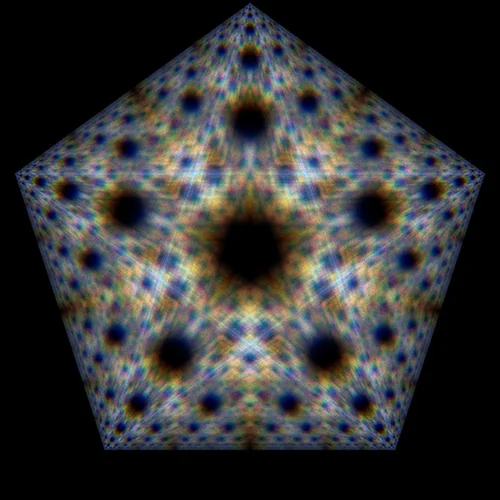n=5, r=0.5, zufällige Punktauswahl

n=5, r=0.5, Eckpunkte können nicht zweimal hintereinander gewählt werden

n=5, r=0.5, Wenn ein Eckpunkt zweimal nacheinander gewählt wird, darf die nächste Wahl kein benachbarter Eckpunkt sein.

Python Quellcode

Die hier beschriebene Implementierung des Zufalls-Iterations-Algorithmus läßt sich in weniger als 80 Zeilen Python-Quellcode implementieren.

import pygame
import random
import math
import colorsys
from pygame.locals import *

idx = [0, 0, 0]

def mark_pixel(surface, pos, pcol):
    col = surface.get_at(pos)
    surface.set_at(pos, (min(col[0] + pcol[0]/10, 255),
                         min(col[1] + pcol[1]/10, 255),
                         min(col[2] + pcol[2]/10, 255)))

def random_point_index(p):
    if len(p) <= 3:
        return random.randint(0, len(p) - 1)

    global idx
    idx[2] = idx[1]
    idx[1] = idx[0]
    dst1 = abs(idx[1] - idx[2])

    while True:
        idx[0] = random.randint(0, len(p) - 1)
        dst = abs(idx[0] - idx[1])
        if dst1 == 0 and (dst == 1 or dst == len(p) - 1):
            continue
        else:
            break

    return idx[0]

def init_polygon(width, height, n):
    delta_angle = 360/n
    r = width/2 - 10
    p = []

    for i in range(0, n):
        angle = (180 + i*delta_angle) * math.pi / 180
        color = colorsys.hsv_to_rgb((i*delta_angle)/360, 0.8, 1)
        p.append(((width/2 + r*math.sin(angle),
                   height/2 + r*math.cos(angle)),
                  (int(color[0]*255), int(color[1]*255), int(color[2]*255))))
    return p

def main(width, height, n, r):
    pygame.init()
    surface = pygame.display.set_mode((width, height))
    pygame.display.set_caption('Das Chaos Spiel')

    p = init_polygon(width, height, n)

    x, y = (400, 300)
    step = 0
    while True:
        step = step + 1
        point_idx = random_point_index(p)

        pos = p[point_idx][0]
        color = p[point_idx][1]
        x += (pos[0] - x) * r
        y += (pos[1] - y) * r

        mark_pixel(surface, (int(x), int(y)), color)

        if step % 1000 == 0:
            pygame.display.update()

        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.image.save(surface, 'chaosspiel.jpg')
                pygame.quit()
                return

if __name__ == "__main__":
    n=5; main(800, 800, n,  0.45)

Dieses Python-Script verwendet die Bibliotheken random, math, colorsys und pygame. Die Bibliothek pygame muss über Pythons Paketmanager PIP installiert werden, bevor das Programm ausgeführt werden kann. Nach den import-Anweisungen wird die globale Variable idx deklariert. Das ist ein Feld, in dem der Index der beiden zuletzte gewählten Polygon-Eckpunkte gespeichert wird. Diese Information ist für die Einschränkung der zufälligen Eckpunktauswahl notwendig.

import pygame
import random
import math
import colorsys
from pygame.locals import *

idx = [0, 0, 0]

Die Funktion mark_pixel bestimmt die Farbe des aktuellen Pixels im Chaosspiel. Die Farbe wird nicht statisch gesetzt. Wenn die Position im Chaosspiel auf ein Pixel fällt, wird dieses jedes mal ein wenig heller gemacht und in der Farbe des Eckpunktes eingefärbt der gewählt wurde um zu dieser Position zu kommen. Dadurch ergeben sich im fertigen Bild schöne Farbübergänge im Fraktal, außerdem werden Pixel, die nicht oft besucht werden dunkler dargestellt.

def mark_pixel(surface, pos, pcol):
    col = surface.get_at(pos)
    surface.set_at(pos, (min(col[0] + pcol[0]/10, 255),
                         min(col[1] + pcol[1]/10, 255),
                         min(col[2] + pcol[2]/10, 255)))

Die Funktion random_point_index wählt einen zufälligen Eckopunkt des Polygones aus und gibt dessen Index zurück. Als Eingabeparameter erhält sie dafür das Fels mit den Polygoneckpunkten. Für eine rein zufällige Punktauswahl würde es reichen, die fett gedruckte Zeile zu verwenden. Die hier dargestellte Variante enthält die Einschränkung, das wenn zweimal der gleiche Eckpunkt gewählt wurde, der nächste Eckpunkt kein direkter Nachbar sein darf.

def random_point_index(p):
    if len(p) <= 3:
        return random.randint(0, len(p) - 1)

	global idx
    idx[2] = idx[1]
    idx[1] = idx[0]
    dst1 = abs(idx[1] - idx[2])

    while True:
        idx[0] = random.randint(0, len(p) - 1)
        dst = abs(idx[0] - idx[1])
        if dst1 == 0 and (dst == 1 or dst == len(p) - 1):
            continue
        else:
            break

    return idx[0]

Die Funktion init_polygon initialisiert die Eckpunkte des Polygones. Als Eingabeparameter erhält sie die Größe des Spielfeldes, sowie die Anzahl der Polygoneckpunkte. Gleichzeitig wird jedem der Eckpunkte des Polygones eine Farbe zugewiesen. Diese Farbe entspricht der Position des Punktes im Farbkreis.

def init_polygon(width, height, n):
    delta_angle = 360/n
    r = width/2 - 10
    p = []

    for i in range(0, n):
        angle = (180 + i*delta_angle) * math.pi / 180
        color = colorsys.hsv_to_rgb((i*delta_angle)/360, 0.8, 1)
        p.append(((width/2 + r*math.sin(angle),
                   height/2 + r*math.cos(angle)),
                  (int(color[0]*255), int(color[1]*255), int(color[2]*255))))
    return p

Die main Funktion ist die Hauptschleife des Programmes. Die Funktion bekommt als Parameter die Größe des Spielfeldes, die Anzahl der Polygoneckpunkte, sowie den Faktor r übergeben, der die Sprunglänge kontrolliert. Hier wird die Grafik initialisiert, die Iteration durchgeführt und nach Abschluss der Berechnungen das Bild abgespeichert. Die aktuelle Position wird in den Variablen x und y abgespeichert.

def main(width, height, n, r):
    pygame.init()
    surface = pygame.display.set_mode((width, height))
    pygame.display.set_caption('Das Chaos Spiel')

    p = init_polygon(width, height, n)

    x, y = (400, 300)
    step = 0
    while True:
        step = step + 1
        point_idx = random_point_index(p)

        pos = p[point_idx][0]
        color = p[point_idx][1]
        x += (pos[0] - x) * r
        y += (pos[1] - y) * r

        mark_pixel(surface, (int(x), int(y)), color)

        if step % 1000 == 0:
            pygame.display.update()

        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.image.save(surface, 'chaosspiel.jpg')
                pygame.quit()
                return

if __name__ == "__main__":
    n=5; main(800, 800, n,  0.45)

Weblinks

Der Youtube-Kanal Numberphile hat ein Video mit Erklärungen zum Chaosspiel veröffentlicht. Darin wird unter anderem auch auf den Barnsley-Farn eingegangen, ein Fraktal das hier nicht näher erläutert werden kann.

Quellenangaben

1. Steffen Polster, "Chaosspiel - Mathematik alpha." auf https://mathematikalpha.de, abgerufen am 2020-05-03
2. Conversano Elisa, Tedeschini Lalli Laura (2011) "Sierpinski Triangles in Stone, on medival floors in Rome." APLIMAT Journal of Applied Mathematics, 4: 114, 122
3. Michael F. Barnsley (1995) "Fraktale. Theorie und Praxis der Deterministischen Geometrie" Spekrum Akademischer Verlag, Heidelberg, ISBN 3-86025-010-8; Seite 96-104