Das Sierpinski-Dreieck und die rekursive Konstruktion von Fraktalen

Verschiedene Fraktale, die mit dem hier beschriebenen Algorithmus erzeugt wurden.

Das Sierpinski-Dreieck

Das Sierpinski-Dreieck tauchte bereits im Chaosspiel auf, wo es durch einen Zufalls-Iterations-Algorithmus erzeugt wurde. Es wird oft als Lehrbeispiel für die Konstruktion selbstähnlicher Mengen verwendet, denn es enthält exakte Kopien seiner selbst egal wie stark man es vergrößert. Die hier beschriebene Methode der Konstruktion basiert auf rekursiven Funktionsaufrufen.

Im ersten Schritt beginnt man mit einem gleichseitigen Dreieck. Im nächsten Schritt wird dieses Dreieck in drei Dreiecke unterteilt, die jeweils halb so groß sind. Der mittlere Teil des Ursprungsdreiecks bleibt leer. Im nächsten Schritt wiederholt man diesen Vorgang. Wenn man das unendlich oft macht, erhält man ein Sierpinski-Dreieck.

Konstruktion eines Spiepinsky-Dreiecks

Das Sierpinski-Dreieck ist eine Art Zwischending zwischen einer Fläche und einer Kurve. Topologisch gesehen spricht man von einem nirgends dichten, lokal zusammenhängenden, metrischen Kontinuum [1]. Mathematisch beschrieben wird das durch die sogenannte Fraktale Dimension. Diese ist für das Sierpinski-Dreieck:

\begin{equation} D = log_2 3 \approx 1.58486... \end{equation}

Also irgendwo zwischen einer Fläche und einer Linie.

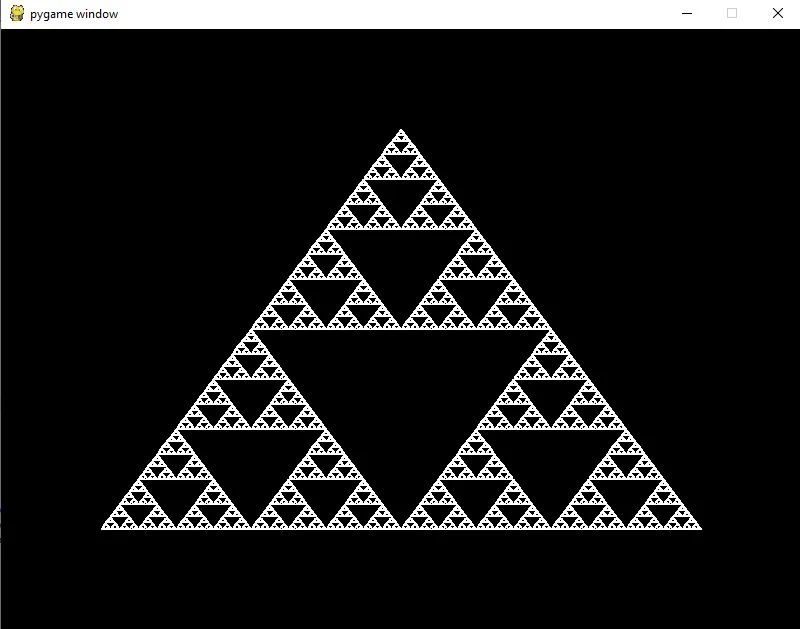Sierpinski-Dreieck berechnet mit dem hier gezeigten Programm.

Quellcode (Sierpinski-Dreieck)

Programmiertechnisch lässt sich dieser Algorithmus in Python in wenigen Zeilen Quellcode umsetzen. Hier wird eine leicht modifizierte Version gezeigt, welche lediglich die Umrisse und keine gefüllten Dreiecke zeichnet. Das macht keinen Unterschied, da alle Algorithmen zur Erzeugung von Sierpinski-Dreiecken am Ende gegen das gleiche Ergebnis konvergieren.

Der Algorithmus startet mit den Eckpunkten eines Dreiecks und unterteilt dieses Dreieck in der subdivide-Funktion in drei kleinere Dreiecke. Dann ruft die subdivide-Funktion sich selbst für jedes der neuen Dreiecke rekursiv auf und wiederholt den Vorgang.

Das Programm bricht nach 9 Unterteilungsschritten ab, weil es zu diesem Zeitpunkt keinen Sinn mehr hat weiter zu unterteilen. Die Dreiecke sind so klein geworden, daß die Computergrafik diese nicht mehr auflösen kann. Das Ergebnis eines Programmdurchlaufs ist im Bild rechts dargestellt. 

import pygame
from pygame.locals import *

def subdivide(surface, p1, p2, p3, level):
    if level >= 9:
        return

    pygame.draw.lines(surface, (255, 255, 255), True, (p1, p2, p3))
    pygame.display.update()

    subdivide(surface, p1, ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2), ((p1[0] + p3[0]) / 2, (p1[1] + p3[1]) / 2), level + 1)
    subdivide(surface, p2, ((p2[0] + p3[0]) / 2, (p2[1] + p3[1]) / 2), ((p2[0] + p1[0]) / 2, (p2[1] + p1[1]) / 2), level + 1)
    subdivide(surface, p3, ((p3[0] + p2[0]) / 2, (p3[1] + p2[1]) / 2), ((p3[0] + p1[0]) / 2, (p3[1] + p1[1]) / 2), level + 1)

def main():
    pygame.init()
    surface = pygame.display.set_mode((800, 600))

    subdivide(surface, (400, 100), (100, 500), (700, 500), 0)

    while True:
        for event in pygame.event.get():
            if event.type == QUIT:
                pygame.quit()
                return

if __name__ == "__main__":
    main()

Der Quellcode dieses Programmes ist in der Datei sierpinski.py des Quellcodearchivs auf GitHub zu sehen.

Verallgemeinerung und Erweiterung der Konstruktionsregeln

Basierend auf dem oben beschriebene Quellcode erweitern wir den Konstruktionsalgorithmus. Die erste Änderung ist, dass wir keine Löcher im Fraktal wie beim klassischen Sierpinski-Dreieck wollen. Daher wird jedes Dreieck in vier kleinere Dreiecke unterteilt, damit seine Fläche komplett ausgefüllt wird.

Darüber hinaus möchten wir Farbe in das Fraktal bringen. Wir weisen daher jedem Eckpunkt des Startdreiecks die Farbe Gelb zu. Dem Dreieck selbst wird die Farbe Rot zugewiesen. Die Farbe der Eckpunkte spielt zunächst beim zeichnen keine Rolle, das Dreieck wird rot gefärbt. Die Eckpunktfarbe kann aber nach bestimmten Regeln in späteren Unterteilungsschritten den untergeordneten Dreiecken zugewiesen werden.

Wenn ein Dreieck unterteilt wird, wird in der Mitte ein neues Dreieck mit den Eckpunkten M, N, O erzeugt. Diese Punkte bekommen die Farbe ihres übergeordneten Dreiecks zugewiesen. Diese Farbe wird zufallsgesteuert leicht aufgehellt. 

def subdivide(v, p, q, r, col, level):
    if level >= 10:
        pixel_col = (min(col[0], 255), min(col[1], 255), min(col[2], 255))
        pygame.draw.polygon(surface, pixel_col, ((int(p.pos[0]), int(p.pos[1])),
                                                 (int(q.pos[0]), int(q.pos[1])),
                                                 (int(r.pos[0]), int(r.pos[1]))))
        return

    col = (randint(col[0], col[0] + 6), randint(col[1], col[1] + 6), randint(col[2], col[2] + 6))
    m = Point(((p.pos[0] + q.pos[0]) / 2, (p.pos[1] + q.pos[1]) / 2), col)
    n = Point(((q.pos[0] + r.pos[0]) / 2, (q.pos[1] + r.pos[1]) / 2), col)
    o = Point(((p.pos[0] + r.pos[0]) / 2, (p.pos[1] + r.pos[1]) / 2), col)

    subdivide(v, m, n, o, p.col if v[0] == 0 else col, level + 1)
    subdivide(v, p, o, m, p.col if v[1] == 0 else col, level + 1)
    subdivide(v, m, n, q, p.col if v[2] == 0 else col, level + 1)
    subdivide(v, o, r, n, p.col if v[3] == 0 else col, level + 1)

Aus den so erhaltenen 6 neuen Punkten P,Q,R,M,N,O werden die vier kleineren Dreiecke ▲M,N,O; ▲P,O,M, ▲M,N,Q und ▲O,R,N gebildet und ihrerseits weiter nach den gleichen Regeln unterteilt. Die Regeln für die Farbzuweisung der neuen Dreiecke stehen im Feld v, das der Funktion subdivide als Parameter übergeben wurde. Dieses Feld enthält vier Einträge, die entweder 1 oder 0 sind.

  • Das Dreieck ▲M,N,O bekommt die Farbe des Punktes P, wenn v[0]==0 ist ansonsten bekommt es gleiche Farbe wie sein übergeordnetes Dreieck
  • Das Dreieck ▲P,O,M bekommt die Farbe des Punktes P, wenn v[1]==0 ist ansonsten bekommt es gleiche Farbe wie sein übergeordnetes Dreieck
  • Das Dreieck ▲M,N,Q bekommt die Farbe des Punktes P, wenn v[2]==0 ist ansonsten bekommt es gleiche Farbe wie sein übergeordnetes Dreieck
  • Das Dreieck ▲O,R,N bekommt die Farbe des Punktes P, wenn v[3]==0 ist ansonsten bekommt es gleiche Farbe wie sein übergeordnetes Dreieck

Die ersten beiden Schritte, sowie die Eckpunktzuweisung in weiteren Schritten der Funktion subdivide für die Regel v = 1, 1, 0, 0 sind in der folgenden Grafik dargestellt:

Das Endergebnis, wenn man mit dieser Regel weiterrechnet, ist eine modifizierte, farbige Version des Sierpinski-Dreiecks.

Das Resultat der Farbverteilungsregel v=1,1,0,0 ist eine farbige Version des Sierpinski-Dreiecks

Die Farbregel v ist ein Feld mit vier Einträgen, die entweder 0 oder 1 sein können. Man kann das auch eine 4 Bit Zahl interpretieren. Es gibt also 2^4 = 16 verschiedene Farbregeln für diesen Konstruktionsmechanismus. Die kompletten Ergebnisse für alle möglichen Farbregeln sind hier dargestellt.

Farbregel v=0,0,0,0
Farbregel v=1,0,0,0
Farbregel v=0,1,0,0
Farbregel v=1,1,0,0
Farbregel v=0,0,1,0
Farbregel v=1,0,1,0
Farbregel v=0,1,1,0
Farbregel v=1,1,1,0
Farbregel v=0,0,0,1
Farbregel v=1,0,0,1
Farbregel v=0,1,0,1
Farbregel v=1,1,0,1
Farbregel v=0,0,1,1
Farbregel v=1,0,1,1
Farbregel v=0,1,1,1
Farbregel v=1,1,1,1

Diese Version des Fraktales ist im Programm triangle_fractal.py des Quellcodearchivs auf GitHub realisiert.

Ist das alles?

Der aufmerksame Leser könnte bemerkt haben, das die Farbgebung nicht nur vom Feld v abhängt, sondern auch von der Punktreihenfolge in den Argumenten der subdivide-Funktion. Für ein Dreieck gibt es 3! = 3*2*1 = 6 verschiedene Möglichkeiten seine Eckpunkte anzuordnen. Aus jedem Dreieck entstehen vier neue Dreiecke. Es gibt also 6*6*6*6 = 1296 verschiedene Möglichkeiten die vier Dreiecke zu unterteilen, wenn die Punktreihenfolge von Bedeutung ist und natürlich gibt es im Algorithmus 16 verschiedene Möglichkeiten der Farbzuweisung. Insgesamt können mit dem Algorithmus nicht nur 16, sondern 1296 * 16 = 20736 verschiedene Fraktale berechnet werden. Viele davon sind zugegebenermaßen einfarbig aber die Vielfalt ist trotzdem enorm.

Im Quellcodearchiv auf GitHub befindet sich eine Programversion namens triangle_fractal_complete.py. Diese berechnete alle möglichen Fraktale für diesen Algorithmus. Eine Auswahl davon ist hier zu sehen:

Quellenangaben

  1. Autorenkollektiv, "Sierpinski-Dreieck." auf https://de.wikipedia.org, abgerufen am 2020-05-12